Categories: Articles destacats » Electricistes novells
Nombre de visualitzacions: 48027
Comentaris sobre l'article: 1
Condensadors de CA
Què és el corrent altern?
Si considerem un corrent directe, no sempre pot ser perfectament constant: la tensió a la sortida de la font pot dependre de la càrrega o del grau de descàrrega de la bateria o de la pila galvànica. Fins i tot amb un voltatge estabilitzat constant, el corrent del circuit extern depèn de la càrrega, cosa que confirma la llei d’Ohm. Resulta que tampoc no és un corrent constant, però tampoc es pot anomenar una corrent variable, ja que no canvia de direcció.
Una variable s’anomena generalment de tensió o corrent, la direcció i la magnitud de les quals no canvia sota la influència de factors externs, com ara una càrrega, sinó que és completament “independent”: així es genera el generador. A més, aquests canvis haurien de ser periòdics, és a dir. repetint-se en un determinat període de temps anomenat període.
Si la tensió o el corrent canvia d’alguna manera, sense preocupar-se de la freqüència i altres regularitats, un senyal s’anomena soroll. Un exemple clàssic és "nevar" en una pantalla de televisió amb un senyal de transmissió feble. A la figura 1 es mostren exemples d'alguns senyals elèctrics periòdics.
Per a corrent directe, només hi ha dues característiques: la polaritat i la tensió de la font. En el cas de corrent altern, aquests dos valors no són suficients, per la qual cosa apareixen diversos paràmetres més: amplitud, freqüència, període, fase, valor instantani i efectiu.
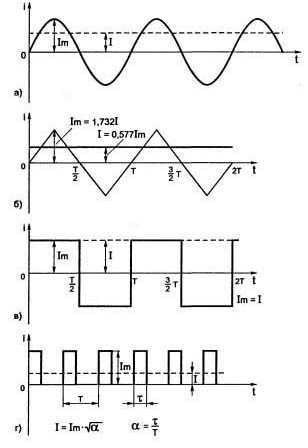
Figura 1Exemples d’alguns senyals elèctrics periòdics
Molt sovint en tecnologia, cal afrontar les oscil·lacions sinusoïdals, a més, no només en enginyeria elèctrica. Imagineu-vos una roda del cotxe. Quan es condueix uniformement per un bon camí suau, el centre de la roda descriu una línia recta paral·lela a la superfície de la carretera. Al mateix temps, qualsevol punt de la perifèria de la roda es desplaça al llarg d’un sinusoide respecte a la línia que s’acaba d’esmentar.
L'esmentat es pot confirmar amb la figura 2, que mostra un mètode gràfic per a construir un sinusoide: qui ha estudiat bé el dibuix sap realitzar aquestes construccions.
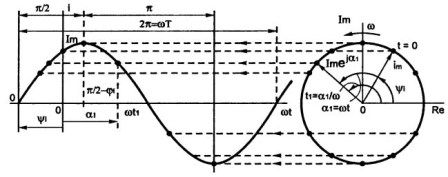
Figura 2Mètode de l’ona del senyal gràfic
Des del curs escolar de física se sap que un sinusoide és el més comú i adequat per estudiar una corba periòdica. Exactament de la mateixa manera, s’obtenen oscil·lacions sinusoïdals a alternadorsa causa del seu dispositiu mecànic.
La figura 3 mostra un gràfic del corrent sinusoïdal.
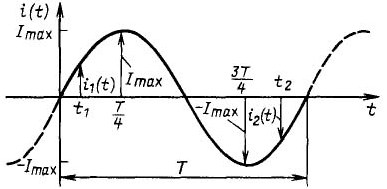
Figura 3Gràfic actual sinusoïdal
És fàcil veure que la magnitud del corrent varia amb el temps, per tant l’eix ordenat s’indica a la figura com i (t), és la funció del corrent versus el temps. El període complet del corrent s’indica amb una línia sòlida i té un període T. Si inicia la consideració des de l’origen, pot veure que al principi la corrent augmenta, arriba a Imax, passa per zero, disminueix a –Imax, després augmenta i arriba a zero. A continuació, comença el següent període, tal com mostra la línia en guix.
En forma de fórmula matemàtica, el comportament actual s’escriu de la manera següent: i (t) = Imax * sin (ω * t ± φ).
Aquí i (t) és el valor instantani del corrent, segons el temps, Imax és el valor d’amplitud (desviació màxima de l’estat d’equilibri), ω és la freqüència circular (2 * π * f), φ és l’angle de fase.
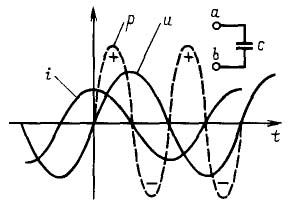
La freqüència circular ω es mesura en radians per segon i l’angle de fase φ en radians o graus. Aquest últim té sentit només quan hi ha dos corrents sinusoïdals. Per exemple, a les cadenes amb condensador el corrent està per davant de la tensió en 90 º o exactament un quart del període, tal com es mostra a la figura 4. Si hi ha un corrent sinusoïdal, llavors el podeu moure per l’eix ordenat com vulgueu, i res no canviarà d’això.
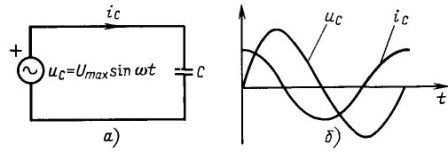
Figura 4 En circuits amb condensador, el corrent se situa per davant de la tensió en un quart de període
El significat físic de la freqüència circular ω és quin angle en els radiians "atravesarà" un sinusoide en un segon.
Període: T és el temps durant el qual l’ona sinusoïdal fa una oscil·lació completa. El mateix s’aplica a vibracions d’una forma diferent, per exemple, rectangulars o triangulars. El període es mesura en segons o unitats més petites: milisegons, microsegons o nanosegons.
Un altre paràmetre de qualsevol senyal periòdic, inclòs un sinusoide, és la freqüència, quantes oscil·lacions farà el senyal en 1 segon. La unitat de mesura de la freqüència és Hertz (Hz), nomenada pel científic del segle XIX Heinrich Hertz. Així doncs, la freqüència d’1 Hz no és més que una oscil·lació / segon. Per exemple, la freqüència de la xarxa d’il·luminació és de 50Hz, és a dir, passen exactament 50 períodes sinusoïdals en un segon.
Si es coneix el període actual (podeu mesura amb un osciloscopi), llavors la freqüència del senyal ajudarà a esbrinar la fórmula: f = 1 / T. A més, si el temps s’expressa en segons, el resultat serà a Hertz. Per contra, T = 1 / f, freqüència en Hz, el temps s’obté en segons. Per exemple, quan 50 hertz el període serà d’1 / 50 = 0,02 segons, o 20 mil·lisegons. En electricitat s’utilitzen més sovint freqüències més elevades: KHz - kilohertz, MHz - megahertz (milers i milions d’oscil·lacions per segon), etc.
Tot el que s'ha dit per a corrent també és cert per a tensió alterna: a la figura 6 n'hi ha prou amb canviar simplement la lletra I a U. La fórmula serà així: u (t) = Umax * sin (ω * t ± φ).
Aquestes explicacions són suficients per tornar-hi experimentar amb condensadors i explicar el seu significat físic.
El condensador condueix corrent altern, que es mostra al diagrama de la figura 3 (vegeu l'article - Condensadors per a instal·lacions elèctriques de corrent altern) La brillantor de la làmpada augmenta quan es connecta un condensador addicional. Quan els condensadors estan connectats en paral·lel, les seves capacitats simplement se sumen, de manera que es pot suposar que la capacitança Xc depèn de la capacitança. A més, també depèn de la freqüència del corrent i, per tant, la fórmula s’assembla així: Xc = 1/2 * π * f * C.
Es desprèn de la fórmula que amb l'augment de la capacitancia i la freqüència de la tensió alterna, la reactància Xc disminueix. Aquestes dependències es mostren a la figura 5.
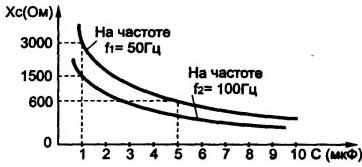
Figura 5. La dependència de la reactància del condensador de la capacitança
Si substituïm la freqüència en Hertz per la fórmula i la capacitança en Farads, el resultat serà a Ohms.
El condensador s’escalfarà?
Ara recorda l’experiència amb un condensador i un comptador elèctric, per què no gira? El fet és que el mesurador considera energia activa quan el consumidor és una càrrega purament activa, per exemple, làmpades incandescents, una caldera elèctrica o una estufa elèctrica. Per a aquests consumidors, la tensió i el corrent coincideixen en fase, tenen un signe: si multipliqueu dos nombres negatius (tensió i corrent durant el semicicle negatiu), el resultat segons les lleis de les matemàtiques continua sent positiu. Per tant, la capacitat d’aquests consumidors sempre és positiva, és a dir. entra a la càrrega i és alliberada en forma de calor, tal com es mostra a la figura 6 per la línia traçada
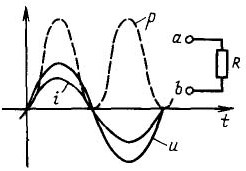
Figura 6
En el cas que el condensador estigui inclòs en el circuit de corrent altern, el corrent i la tensió no coincideixen en fase: el corrent és de 90 μ per davant de la fase en la tensió, el que condueix a una combinació quan el corrent i la tensió tenen signes diferents.
Figura 7
En aquests moments, la potència és negativa. És a dir, quan la potència és positiva, el condensador es carrega i, quan és negatiu, l’energia emmagatzemada es torna a transferir a la font. Per tant, de mitjana resulta zero i simplement no hi ha res a comptar aquí.
El condensador, llevat que sigui útil, ni tan sols s'escalfarà. Per tant, sovint condensador anomenat resistència lliure, que permet el seu ús en fonts d'alimentació de baix consum sense transformació.Tot i que aquests blocs no es recomanen pel seu perill, de vegades cal fer-ho.
Abans d'instal·lar-lo en aquesta unitat condensador d’apagament, s'ha de comprovar mitjançant una simple connexió a la xarxa: si en mitja hora el condensador no s'ha escalfat, pot incloure's al circuit de forma segura. En cas contrari, només caldrà llençar-lo sense penediment.
Què mostra un voltímetre?
En la fabricació i reparació de diversos aparells, encara que no gaire sovint, cal mesurar tensions i corrents alterns. Si un sinusoide es comporta de manera tan agitada, cap amunt i avall, què mostrarà un voltímetre normal?
El valor mitjà d’un senyal periòdic, en aquest cas un sinusoide, es calcula com l’àrea delimitada per l’eix abscisa i la imatge gràfica del senyal dividida en 2 * π radians o el període del sinusoide. Com que les parts superior i inferior són absolutament idèntiques, però presenten signes diferents, el valor mitjà del sinusoide és zero, i no cal mesurar-lo en absolut, i fins i tot és senzillament sense sentit.
Per tant, el dispositiu de mesura ens mostra el valor rms de tensió o corrent. El valor quadrat mitjà és un valor del corrent periòdic en què es desprèn la mateixa quantitat de calor en la mateixa càrrega que en corrent directe. És a dir, la bombeta brilla amb la mateixa brillantor.
Això ho descriu les fórmules com aquesta: Icrc = 0,707 * Imax = Imax / √2 per a tensió, la fórmula és la mateixa, només cal canviar una lletra Ucrc = 0,707 * Umax = Umax / √2. Són aquests valors els que mostra el dispositiu de mesura. Es poden substituir en fórmules quan es calcula segons la llei d’Ohm o quan es calcula la potència.
Però no és tot el que és capaç un condensador en una xarxa de CA. En el proper article, considerarem l’ús de condensadors en circuits polsats, filtres de pas alt i baix pas, en generadors d’ona sinusoïdal i d’ona quadrada.
Boris Aladyshkin
Continuació de l'article: Condensadors en circuits electrònics
Consulteu també a electro-ca.tomathouse.com
: