Categories: Articles destacats » Electrònica pràctica
Nombre de visualitzacions: 124786
Comentaris sobre l'article: 1
Realització d'una mesurament dels oscil·loscopis
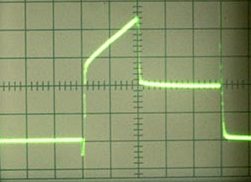Per descomptat, un osciloscopi digital és molt més perfecte que un electrònic convencional, permet recordar formes d'ona, connectar-se a un ordinador personal, tenir processament matemàtic de resultats, marcadors de pantalla i molt més. Però, amb tots els avantatges, aquests dispositius de nova generació tenen un important inconvenient: és un preu elevat.
És ella qui fa que l’oscil·loscopi digital sigui inaccessible amb finalitats aficionades, tot i que hi ha oscil·loscopis “de butxaca” per valor de només uns quants milers de rubles, que es venen a Aliexpress, però no és especialment convenient utilitzar-los. Bé, només una joguina interessant. Per tant, mentre parlarem de mesures mitjançant un osciloscopi electrònic.
Podeu trobar un nombre suficient de fòrums sobre el tema de l'elecció d'un osciloscopi per utilitzar-lo en un laboratori domèstic a Internet. Sense negar els avantatges dels osciloscopis digitals, es recomana en molts fòrums que opti per oscil·loscopis domèstics senzills, de mida petita i fiable C1-73 i C1-101 i similars, que ja vam conèixer anteriorment aquest article.
Amb un preu bastant assequible, aquests dispositius us permetran realitzar la majoria de tasques de ràdio aficionades. Mentrestant, coneixem els principis generals de les mesures mitjançant un osciloscopi.
Figura 1. Oscil·loscopi S1-73
Què mesura un osciloscopi
El senyal mesurat s’alimenta a l’entrada del canal de desviació vertical Y, que té una gran resistència d’entrada, generalment 1MΩ, i una petita capacitat de entrada, no superior a 40pF, que permet introduir una distorsió mínima al senyal mesurat. Aquests paràmetres se solen indicar al costat de l'entrada del canal de desviació vertical.
Figura 2. Oscil·loscopi C1-101
L’alta impedància d’entrada és típica dels voltímetres, per la qual cosa es pot dir que l’oscil·loscopi mesura la tensió. L’ús de divisors d’entrada externs permet reduir la capacitança d’entrada i augmentar la impedància d’entrada. També redueix la influència de l’oscil·loscopi sobre el senyal que s’està investigant.
Cal recordar que hi ha osciloscopis especials d’alta freqüència, la impedància d’entrada dels quals és només de 50 ohms. En la pràctica de ràdio aficionada, aquests dispositius no troben aplicació. Per tant, ens centrarem més en osciloscopis universals convencionals.
Amplada de banda del canal Y
L’osciloscopi mesura voltatges en un rang molt ampli: des de tensions de corrent continu fins a tensions d’una freqüència prou alta. El balanceig de tensió pot ser força divers, des de desenes de millivolts fins a desenes de volts i quan s’utilitzen divisors externs fins a diversos centenars de volts.
Cal tenir en compte que l’ample de banda del canal de la desviació vertical Y db no menys de 5 vegades superior a la freqüència del senyal a mesurar. És a dir, l'amplificador de la desviació vertical ha de passar com a mínim el cinquè harmònic del senyal estudiat. Això és especialment necessari per estudiar polsos rectangulars que contenen molts harmònics, tal com es mostra a la figura 3. Només en aquest cas s’obté una imatge amb una distorsió mínima a la pantalla.
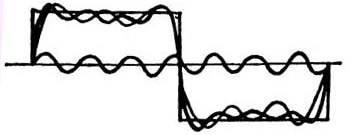
Figura 3. Síntesi d’un senyal rectangular de components harmònics
A més de la freqüència fonamental, la figura 3 mostra el tercer i el setè harmònic. A mesura que el nombre harmònic augmenta, la seva freqüència augmenta: la freqüència del tercer harmònic és tres vegades superior a la fonamental, la cinquena harmònica és cinc vegades, la setena és set, etc. D’acord amb això, l’amplitud dels harmònics superiors disminueix: com més gran sigui el nombre harmònic, menor serà la seva amplitud. Només si l'amplificador del canal vertical sense molta atenuació pot perdre els armònics superiors, la imatge del pols serà rectangular.
La figura 4 mostra la forma d’ona d’un meandre amb amplada de banda de canal Y insuficient.
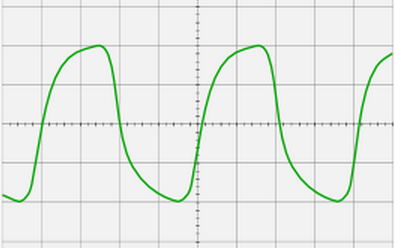
Figura 4
El meandre amb una freqüència de 500 KHz sembla una cosa així a la pantalla d’un oscil·loscopi OMSh-3M amb un ample de banda de 0 ... 25 KHz. Com si passessin polsos rectangulars a través d’un circuit RC integrador. Aquest osciloscopi va ser produït per la indústria soviètica per a treballs de laboratori en lliçons de física a les escoles. Fins i tot la tensió d’alimentació d’aquest dispositiu per motius de seguretat no era de 220, sinó només de 42V. És absolutament obvi que un osciloscopi amb un ample de banda permetrà observar un senyal amb freqüències no superiors a 5 kHz sense gairebé cap distorsió.
Per a un osciloscopi universal convencional, l'amplada de banda és sovint de 5 MHz. Fins i tot amb una banda d’aquest tipus, es pot veure un senyal de fins a 10 MHz i superior, però la imatge rebuda a la pantalla permet jutjar només la presència o absència d’aquest senyal. Serà difícil dir res sobre la seva forma, però en algunes situacions la forma no és tan important: per exemple, hi ha un generador d’ona sinusoïdal i n’hi ha prou només per assegurar-se que hi ha aquesta ona sinusoïdal o no. A la figura 4 es mostra una situació així.
Els sistemes informàtics moderns i les línies de comunicació operen a freqüències molt altes, de l'ordre de centenars de megavarts. Per veure aquests senyals d’alta freqüència, l’ample de banda de l’oscil·loscopi ha de ser com a mínim de 500 MHz. Una banda tan ampla realment “amplia” el preu de l’osciloscopi.
Un exemple és l’oscil·loscopi digital U1610A que no es mostra a la figura 5. El seu ample de banda és de 100 MHz i el preu és de gairebé 200.000 rubles. D’acord, no tothom es pot permetre el luxe de comprar un dispositiu tan car.
Figura 5
Que el lector no consideri aquesta imatge com a anunci publicitari, ja que no es reprodueixen totes les coordenades del venedor: hi ha cap captura de pantalla similar al lloc d'aquesta imatge.
Tipus de senyals estudiats i els seus paràmetres
El tipus d’oscil·lació més comú a la natura i la tecnologia és un sinusoide. Aquesta és la mateixa funció que pateix molt de temps Y = sinX, que es va celebrar a l'escola en els aprenentatges de la trigonometria. Molts processos elèctrics i mecànics tenen una forma sinusoïdal, tot i que sovint s’utilitzen altres formes de senyals en tecnologia electrònica. Alguns d’ells es mostren a la figura 6.
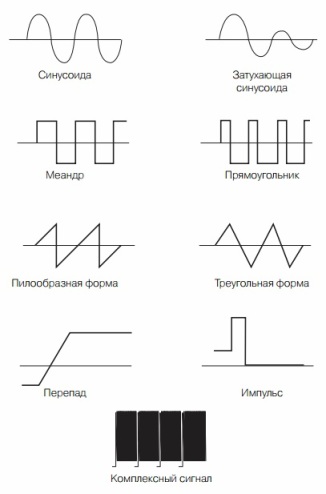
Figura 6. Formes de vibracions elèctriques
Senyals periòdics. Característiques del senyal
Un osciloscopi electrònic universal permet estudiar amb precisió els senyals periòdics. Si, a l’entrada Y, envieu un senyal de so real, per exemple, un fonograma musical, aleshores es mostraran explosions de parpelleig aleatòries a la pantalla. Naturalment, és impossible investigar amb detall aquest senyal. En aquest cas, ajudarà l’ús d’un osciloscopi d’emmagatzematge digital, que permet estalviar la forma d’ona.
Les oscil·lacions mostrades a la figura 6 són periòdiques, que es repeteixen després d’un cert període de temps T. Això es pot considerar amb més detall a la figura 7.
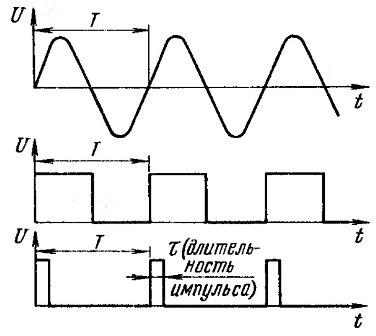
Figura 7. Fluctuacions periòdiques
Les oscil·lacions es mostren en un sistema de coordenades bidimensional: la tensió es mesura al llarg de l’eix ordenat i el temps es mesura al llarg de l’eix abscisa. El voltatge es mesura en volts i el temps en segons. Per a vibracions elèctriques, el temps es mesura sovint en mil·lisegons o microsegons.
A més dels components X i Y, la forma d'ona també conté la intensitat del component Z, o simplement lluentor (figura 8). És ella qui encén el feix durant el temps de cursa avançada del feix i s’extingeix per l’hora de tornada. Alguns osciloscopis tenen una entrada per controlar la brillantor, que s’anomena entrada Z. Si s’aplica una tensió d’impuls d’un generador exemplar a aquesta entrada, es poden veure etiquetes de freqüència a la pantalla. Això permet mesurar amb més precisió la durada del senyal al llarg de l’eix X.
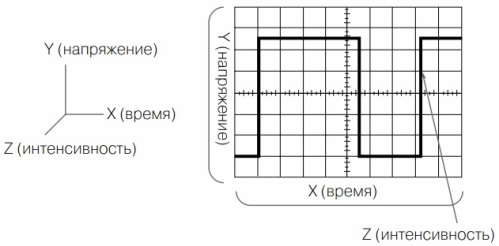
Figura 8. Tres components del senyal investigat
Els osciloscopis moderns tenen, per regla general, escombrats calibrats pel temps que permeten una sincronització precisa. Per tant, pràcticament no és necessari utilitzar un generador extern per crear etiquetes.
A la part superior de la figura 7 hi ha una ona sinusoïdal. És fàcil veure que comença al començament del sistema de coordenades. Durant el temps T (període), es realitza una oscil·lació completa. Després tot es repeteix, el període següent. Aquests senyals s’anomenen periòdics.
Els senyals rectangulars es mostren a sota de l’ona sinusoïdal: meandre i pols rectangular. També són periòdics amb el període T. La durada del pols es denota com a τ (tau). En el cas d'un meandre, la durada del pols τ és igual a la durada de la pausa entre polsos, només la meitat del període T. Per tant, el meandre és un cas especial d'un senyal rectangular.
Taxa de treball i impost
Per caracteritzar els polsos rectangulars, s’utilitza un paràmetre anomenat cicle de treball. Aquesta és la relació del període de repetició del pols T a la durada del pols τ. Per al meandre, el cicle de treball és igual a dos, - el valor és sense dimensions: S = T / τ.
A la terminologia anglesa, és just el contrari. Allà, els polsos es caracteritzen pel cicle de treball, la relació de la durada del pols al període del cicle de treball: D = τ / T. El factor d’ompliment s’expressa en %%. Així, per al meandre, D = 50%. Resulta que D = 1 / S, cicle de treball i cicle de treball són mutuament inversos, tot i que caracteritzen el mateix paràmetre de pols. La forma d'ona del meandre es mostra a la figura 9.
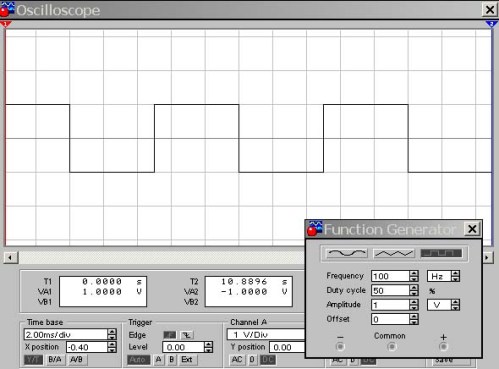
Figura 9. Forma d’ona del meandre D = 50%
Aquí, l’entrada de l’oscil·loscopi està connectada a la sortida del generador funcional, que es mostra immediatament a la cantonada inferior de la figura. I aquí un lector atent pot fer una pregunta: “L’amplitud del senyal de sortida del generador d’1V, la sensibilitat de l’entrada de l’oscil·loscopi és d’1V / div. I la pantalla mostra polsos rectangulars amb una magnitud de 2V. Per què?
El fet és que el generador funcional genera polsos rectangulars bipolars respecte al nivell de 0V, aproximadament el mateix que un sinusoide, amb amplituds positives i negatives. Per tant, a la pantalla de l’oscil·loscopi s’observen polsos amb un interval de ± 1V. A la figura següent, canviem el cicle de treball, per exemple, al 10%.
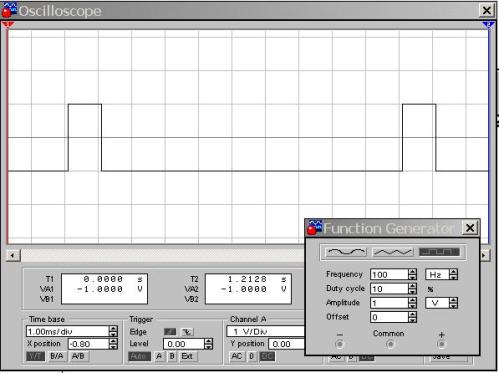
Figura 10. Moment rectangular D = 10%
És fàcil veure que el període de repetició del pols és de 10 cèl·lules, mentre que la durada del pols és només d’una cèl·lula. Per tant, D = 1/10 = 0,1 o 10%, com es pot veure a la configuració del generador. Si utilitzeu la fórmula per calcular el cicle de treball, obtindreu S = T / τ = 10/1 = 1: el valor és sense dimensions. Aquí podem concloure que el cicle de treball caracteritza l’impuls molt més clarament que el cicle de treball.
En realitat, el senyal en va seguir igual que a la figura 9: un pols rectangular amb una amplitud d’1 V i una freqüència de 100 Hz. Només canvia el factor d’ompliment o el cicle de treball, com si algú sigui més familiar i convenient. Però, per la comoditat de l'observació de la figura 10, la durada de l'exploració es redueix a la meitat en comparació amb la figura 9 i és d'1ms / div. Per tant, el període de senyal té 10 cel·les a la pantalla, cosa que facilita la comprovació que el cicle de treball sigui del 10%. Quan s'utilitza un osciloscopi real, la durada del barrat es selecciona aproximadament la mateixa.
Mesurament de tensió de pols rectangular
Com s'ha esmentat al començament de l'article, l'osciloscopi mesura la tensió, és a dir. diferència de potencial entre dos punts. Típicament, les mesures es prenen en relació amb un cable comú, a terra (zero volts), tot i que això no és necessari. En principi, és possible mesurar de mínims a màxims valors de senyal (valor pic, pic a pic). En qualsevol cas, els passos de mesurament són força senzills.
Els polsos rectangulars són sovint unipolars, cosa típica per a la tecnologia digital. A la figura 11 es mostra com es mesura la tensió d’un pols rectangular.
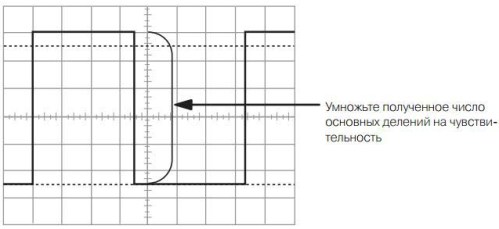
Figura 11. Mesura de l'amplitud d'un pols rectangular
Si la sensibilitat del canal de desviació vertical és d'1 V / div, resulta que la figura mostra un pols amb un voltatge de 5,5 V. Amb una sensibilitat de 0,1 V / div. La tensió serà només de 0,5V, tot i que a la pantalla tots dos polsos semblen exactament iguals.
Què més es pot veure en un impuls rectangular
Els polsos rectangulars que es mostren a les figures 9, 10 són simplement ideals perquè són sintetitzats per Electronics WorkBench. I la freqüència d’impulsos només és de 100 Hz, per tant, no poden sorgir problemes amb la “agudesa” de la imatge. En un dispositiu real, a un ritme elevat de repetició, els polsos són una mica distorsionats, en primer lloc, apareixen diverses sobretensions i ràfegues a causa de la inductància de la instal·lació, com es mostra a la figura 12.
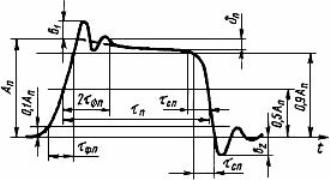
Figura 12. Impuls real rectangular
Si no es presta atenció a aquestes "truques", l'impuls rectangular es veu com el que es mostra a la figura 13.
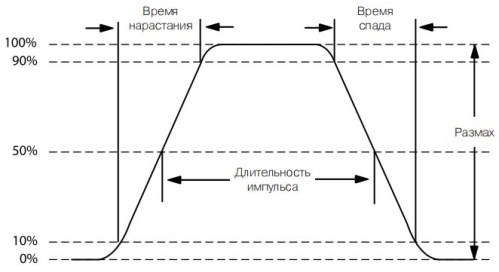
Figura 13. Paràmetres d’un pols rectangular
La figura mostra que les vores capçals i posteriors del pols no apareixen immediatament, però tenen uns temps de pujada i caiguda, i són una mica inclinats respecte a la línia vertical. Aquest pendent es deu a les propietats de freqüència de microcircuits i transistors: com més gran sigui el transistor de freqüència, menys “fronts” dels polsos. Per tant, la durada del pols està determinada pel nivell del 50% del rang complet.
Per la mateixa raó, l'amplitud del pols està determinada pel nivell del 10 ... 90%. La durada del pols, així com la tensió, es determina multiplicant el nombre de divisions de l'escala horitzontal pel valor de divisió, tal com es mostra a la figura 14.
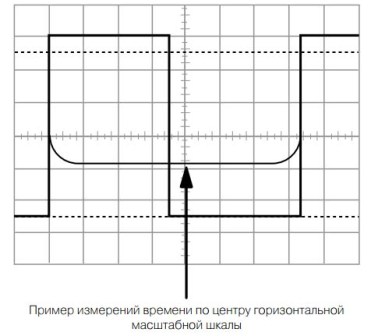
Figura 14.
La figura mostra un període d’un pols rectangular, lleugerament diferent del meandre: la durada d’un pols positiu és de 3,5 divisions de l’escala horitzontal i la durada de la pausa és de 3,8 divisions. El període de repetició de pols és de 7,3 divisions. Aquesta imatge pot pertànyer a diversos polsos diferents amb freqüències diferents. Tot dependrà de la durada de l'escombrat.
Assumeix una durada d’escaneig d’1ms / div. Aleshores el període de repetició del pols és de 7,3 * 1 = 7,3ms, que correspon a la freqüència F = 1 / T = 1 / 7,3 = 0,1428KHz o 143 Hz. Si la durada de l'escaneig és d'1 µs / div, la freqüència resultarà ser mil vegades superior, és a dir, 143KHZ.
Si usem les dades de la figura 14, no és difícil calcular el cicle de funcionament del pols: S = T / τ = 7,3 / 3,5 = 2,0857, resulta gairebé com un meandre. Cicle de treball cicle de treball D = τ / T = 3,5 / 7,3 = 0,479 o 47,9%. Cal tenir en compte que aquests paràmetres no depenen en cap cas de la freqüència: el cicle de treball i el cicle de treball es calculaven simplement per divisions de la forma d'ona.
Amb impulsos rectangulars, tot sembla ser clar i senzill. Però ens oblidem completament de l’ona sinusoïdal. De fet, hi ha el mateix: podeu mesurar tensions i paràmetres de temps. A la figura 15 es mostra un període d'ona sinusoïdal.
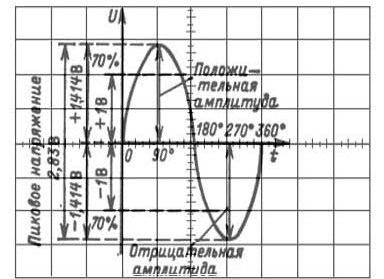
Figura 15. Paràmetres d’ona sinusoïdal
Bviament, pel sinusoide mostrat a la figura, la sensibilitat del canal de desviació vertical és de 0,5 V / div. Els paràmetres restants es poden determinar fàcilment multiplicant el nombre de divisions per 0,5 V / div.
L’ona sinusoïdal pot ser una altra, que s’haurà de mesurar amb sensibilitat, per exemple, 5V / div. Aleshores en lloc de 1V obtens 10V. Tanmateix, a la pantalla, la imatge de tots dos sinusoides sembla exactament la mateixa.
Es desconeix el calendari del sinusoide mostrat. Si suposem que la durada de l’exploració és de 5ms / div, el període serà de 20ms, que correspon a una freqüència de 50Hz. Les xifres en graus de l’eix temporal indiquen la fase del sinusoide, tot i que això no és particularment important per a un sol sinusoide. Més sovint és necessari determinar el desplaçament de fase (directament en mil·lisegons o microsegons) com a mínim entre dos senyals. Això es fa millor amb un osciloscopi de dos feixos. Com es fa així es mostra a continuació.
Com es mesura el corrent amb un osciloscopi
En alguns casos, cal fer una mesura de la magnitud i la forma del corrent. Per exemple, el corrent altern que circula per un condensador és per davant de la tensió per ¼ període. Aleshores, s’inclou al circuit obert una resistència amb una resistència petita (dècimes d’un Ohm). Aquesta resistència no afecta el funcionament del circuit. La caiguda de tensió a través d’aquest resistor mostrarà la forma i la magnitud del corrent que circula pel condensador.
Un amperímetre de calibre similar està disposat de la mateixa manera aproximadament, que s'inclourà en la ruptura del circuit elèctric. En aquest cas, la resistència de mesura es troba dins del mateix amperímetre.
A la figura 16 es mostra el circuit per mesurar el corrent a través del condensador.
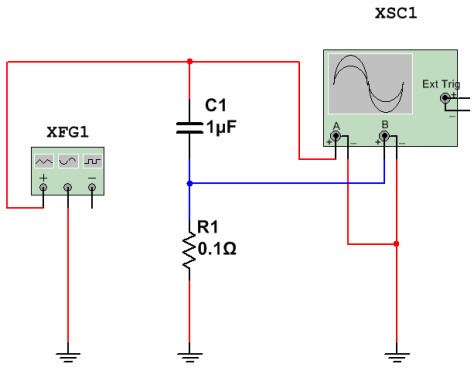
Figura 16. Mesura de corrent mitjançant un condensador
Una tensió sinusoïdal de 50 Hz amb una amplitud de 220 V del generador XFG1 (feix vermell a la pantalla de l’oscil·loscopi) s’ofereix al circuit sèrie des del condensador C1 i la resistència de mesura R1. La caiguda de tensió a través d’aquest resistor mostrarà la forma, la fase i la magnitud del corrent a través del condensador (feix blau). Com es veu a la pantalla de l’oscil·loscopi es mostra a la figura 17.
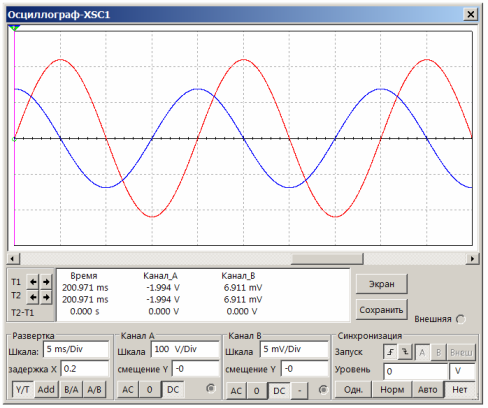
Figura 17. El corrent que passa pel condensador és per davant de la tensió per ¼ període
Amb una freqüència d’ona sinusoïdal de 50 Hz i un temps d’escaneig de 5 ms / Div, un període d’ona sinusoïdal té 4 divisions al llarg de l’eix X, molt convenient per a l’observació. És fàcil veure que el raig blau està per davant del vermell exactament amb una divisió al llarg de l’eix X, que correspon a ¼ període. Dit d’una altra manera, el corrent a través del condensador està per davant del voltatge de fase, que és totalment coherent amb la teoria.
Per calcular el corrent a través del condensador, n’hi ha prou amb fer servir la llei d’Ohm: I = U / R. Quan la resistència de la resistència de mesura és de 0,1 ohm, la caiguda de tensió al seu voltant és de 7 mV. Aquest és el valor de l'amplitud. Aleshores, el corrent màxim a través del condensador serà de 7 / 0,1 = 70 mA.
Mesurar la forma del corrent a través del condensador no és cap tasca molt urgent, tot és clar i sense mesuraments. En lloc d’un condensador, hi pot haver qualsevol càrrega: inductor, bobinatge del motor, estadi amplificador de transistors i molt més. És important que es pugui fer servir aquest mètode per estudiar el corrent, que en alguns casos difereix de forma significativa entre la forma i la tensió.
Boris Aladyshkin
Consulteu també a electro-ca.tomathouse.com
: