Categories: Articles destacats » Electrònica pràctica
Nombre de visualitzacions: 32001
Comentaris sobre l'article: 2
Condensadors en circuits electrònics
En articles anteriors, hem parlat breument sobre el funcionament dels condensadors en circuits de CA, com i per què els condensadors passen corrent altern (vegeu - Condensadors de CA) En aquest cas, els condensadors no s’escalfen, no s’hi destina potència: en una mitja onada del sinusoide, el condensador es carrega i, en l’altre, es descarrega de forma natural, mentre es transfereix l’energia emmagatzemada de nou a la font actual.
Aquest mètode de pas de corrent permet anomenar el condensador a una resistència lliure i, per això, el condensador connectat a la sortida no fa girar el comptador. I tot això és degut a que la corrent del condensador és per davant d’1 / 4 del temps que s’hi aplica la tensió.
Però aquest avenç de fase fa possible no només “enganyar” el comptador, sinó que permet crear diversos circuits, per exemple, generadors de senyals sinusoïdals i rectangulars, retards en temps i diversos filtres de freqüència.
En el procés d’aquesta història, caldrà recordar de vegades el que ja s’ha dit abans, per dir-ho, resumir. Això ajudarà a no tornar a articles anteriors per recordar una fórmula senzilla, o simplement, "què és?"
Connexió en sèrie i paral·lela de condensadors
Amb una connexió paral·lela de condensadors, la capacitat total és simplement la suma aritmètica de les capacitats. Naturalment, amb aquesta inclusió, la capacitança total serà superior a la capacitat del condensador més gran. Ctotal = C1 + C2 + C3 + ... + Cn.
En el cas d'una connexió en sèrie, la capacitat total és inferior a la de la més petita.
1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
Quan es connecten dos condensadors idèntics en sèrie, la capacitança total serà igual a la meitat de la capacitança d’un: per exemple, en connectar dos condensadors d’1 µF cadascun, la capacitança total serà de 0,5 µF.
Capacitança Xc
Aquí, tot, com quan es connecten resistències, només és exactament el contrari: una connexió en sèrie redueix la capacitança total, mentre que una paral·lela la augmenta. Aquesta circumstància no s'ha d'oblidar quan es connecten condensadors, ja que un augment de la capacitança condueix a una disminució de la capacitança Xc
Xc = 1/2 * π * f * C
Des del punt de vista de les matemàtiques, això és força natural, perquè la capacitat C es troba en el denominador de la fracció. Per cert, la freqüència f està al mateix lloc, de manera que un augment de la freqüència també comporta una disminució de la capacitança Xc. El significat físic d’això és que a través del mateix condensador és millor, més sense obstacle, que passin altes freqüències. Això es parlarà una mica més endavant, quan es tracti de filtres de pas baix i de pas alt.
Si agafem un condensador amb una capacitat d’1 μF, llavors per a una freqüència de 60 Hz el seu Xc serà de 2653 Ohms, i per a una freqüència de 400 Hz el mateix condensador té una Xc de només 398 Ohms. Aquells que ho desitgin poden consultar aquests resultats mitjançant la fórmula, substituint π = 3.14, la freqüència en hertz i la capacitança en els farads. Aleshores, el resultat serà en ohms. Tot ha de complir el sistema SI.
Però els condensadors no només s’utilitzen com a resistències d’amortiment lliure o en filtres de rectificació. Sense la seva participació, circuits per a generadors de baixa i alta freqüència, diversos convertidors de forma d'ona, diferenciant i integrant circuits, amplificadors i altres esquemes.
A continuació, es tindran en compte diversos senyals elèctrics amb els quals han de treballar els condensadors. En primer lloc, es tracta de senyals periòdiques adequades per a la seva observació osciloscopi.
Període i freqüència d’oscil·lacions
Per tant, s’anomena periòdica una oscil·lació que, sense cessar, repeteix la mateixa forma, per exemple, una oscil·lació sinusoïdal. La durada d’aquest desenvolupament complet s’anomena precisament el període T i es mesura en segons, mil·lisegons, microsegons.L’electrònica moderna fins i tot tracta de nanosegons (un mil·lèsima de segon).
El nombre de períodes per segon s’anomena freqüència (amb quina freqüència) de les oscil·lacions f i s’expressa en hertz. 1Hz és la freqüència en què es realitza una oscil·lació, un període complet, en 1 segon. La relació del període i la freqüència s’expressa mitjançant la fórmula simple T = 1 / f.
D’acord amb això, coneixent el període d’oscil·lació, és molt senzill calcular la freqüència f = 1 / T.
Així es calcula la freqüència quan es mesura amb un osciloscopi: es calcula el nombre de cèl·lules en un període, multiplicat per la durada d’una cèl·lula i el període s’obté, per exemple, en microsegons. I per conèixer la freqüència, simplement van utilitzar la darrera fórmula.
Ordinària osciloscopi electrònic Permet obtenir només senyals periòdiques que es poden sincronitzar amb la freqüència d'escombratge per obtenir una imatge fixa adequada per a la investigació. Si envieu un senyal a un programa de música a l’entrada de l’oscil·loscopi, no podreu parar la imatge per res. Per observar aquests senyals, s’utilitzen osciloscopis d’emmagatzematge.
Quan un període es mesura en mil·lisegons, la freqüència s’obté en quilohertz, durant un període mesurat en microsegons, la freqüència ja s’expressa en megahertz. Això és així si no seguiu els requisits del sistema SI: període en segons, freqüència en hertz.
Vibracions no sinusoïdals
Com s'ha esmentat anteriorment, l'ona sinusoïdal és la més comuna i adequada per a l'estudi i l'ús pràctic de la corba periòdica. En condicions industrials, s’obté mitjançant generadors elèctrics, per exemple, en centrals hidroelèctriques. Als dispositius electrònics s’utilitzen vibracions de les més diverses formes.
Es tracta bàsicament de tres formes: sinusoïdal, rectangular i triangular, com es mostra a la figura 1. Tant el corrent com la tensió poden tenir una forma, per tant, només es mostra l’eix del temps a la figura, l’eix ordenat es queda sense un nom.
Aquestes oscil·lacions són generades per circuits electrònics especials. Els senyals rectangulars i triangulars s’anomenen sovint polsats. Tot i això, hi ha molts circuits electrònics que realitzen conversió de senyal: per exemple, un rectangle, un triangle es pot fer a partir d’un sinusoide.
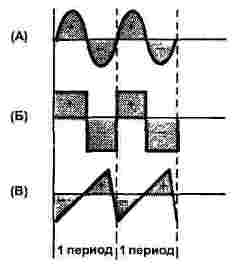
Figura 1
Per als tres senyals, la figura mostra dos períodes, tots els senyals tenen la mateixa freqüència.
Espectre de senyals no sinusoïdals
Qualsevol senyal elèctric es pot representar com una mesura de l'amplitud en algun moment del temps. La freqüència d’aquestes mostres s’anomena freqüència de mostreig i almenys dues vegades superior a la freqüència superior del senyal mesurat. A partir d’aquestes mostres, podeu restaurar el senyal original. Aquest mètode s'utilitza, per exemple, en l'enregistrament digital de so. Aquest mètode també s’anomena anàlisi del temps.
Un altre mètode suposa que qualsevol senyal, fins i tot un rectangular, es pot representar com la suma algebraica de sinusoides amb diferents freqüències i fases. Aquest mètode s’anomena anàlisi de freqüència. Però, el que es deia “amb freqüències diferents” no és del tot cert: els sinusoides constituents s’anomenen harmònics i les seves freqüències obeeixen certes lleis.
Una ona sinusoïdosa la freqüència de la qual és igual a la freqüència d’una ona quadrada s’anomena fonamental o primer harmònic. Fins i tot els harmònics s’obtenen multiplicant la freqüència fonamental per un nombre parell, i els harmònics parells, respectivament, per parell.
Així, si el primer harmònic té una freqüència de 1000 Hz, llavors el segon és de 2000 Hz, el quart és de 4000 Hz, etc. Els harmònics estranys tindran freqüències de 3000Hz, 5000Hz. D'altra banda, cada harmònica és més petita en amplitud que la principal: com més gran és l'harmònica, menor serà l'amplitud.
En música, els harmònics s’anomenen sobretensions. Són ells els que formen el timbre del so, permeten distingir el violí del piano i la guitarra del saxo. No permeten confondre la veu masculina i la femenina ni distingir Petrov d’Ivanov. I només el sinusoide en si ja no es pot descompondre ni muntar des de cap senyal.
La figura 2 mostra la construcció d’un pols rectangular.
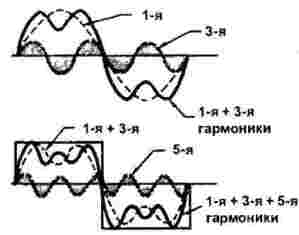
Figura 2
El primer i el tercer harmònic es mostren a la part superior de la figura. És fàcil veure que en un període del primer harmònic tres períodes de la tercera passada. En aquest cas, l’amplitud del tercer harmònic és un terç del primer. Aquí també es mostra la suma dels primers i del tercer harmònics.
A continuació, juntament amb la suma d’1 i 3 harmònics, es mostren altres 5 harmònics: per a un període d’un senyal rectangular aconsegueix fer exactament cinc períodes. En aquest cas, la seva amplitud és encara més petita i, més exactament, exactament 1/5 del principal (primer). Però no s'hauria de pensar que tot acabi amb el cinquè harmònic: simplement no es pot mostrar a la figura, de fet n'hi ha molt més.
La formació de senyals dentats i triangulars, mostrats a la figura 3, és una mica més complicada: si en el cas anterior només hi van participar armònics imparells, entran en joc fins i tot els harmònics.
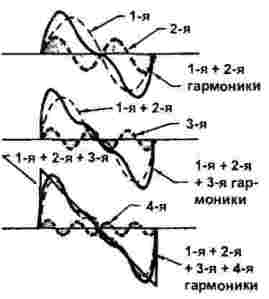
Figura 3
Així, podem afirmar que amb l'ajuda de molts harmònics es sintetitza un senyal de qualsevol forma i que el nombre i el tipus d'harmònics depenen de la forma d'ona, tal com es mostra a les figures 2 i 3.
En reparar i muntar equips electrònics, s’utilitza un osciloscopi per estudiar senyals elèctrics. Permet considerar la forma de senyals periòdics, la seva amplitud, mesurar el període de repetició. Però els harmònics mostrats a les figures 2 i 3 no es poden veure.
Tot i que connecteu, per exemple, una guitarra elèctrica a un osciloscopi, tireu una cadena, apareix un sinusoide a la pantalla, és el primer harmònic. En aquest cas, no es pot parlar de detalls. Es produirà el mateix sinusoide si bufes a la canonada o flauta davant del micròfon.
Com obtenir impulsos rectangulars
Després de conèixer els senyals elèctrics, hem de recordar els condensadors amb els quals va començar l'article. En primer lloc, heu de conèixer un dels circuits clàssics d’electrònica - multivibrador, (Figura 4) és ell qui genera polsos rectangulars. El circuit és tan clàssic que comença a funcionar de seguida sense requerir ajustaments ni ajustaments.
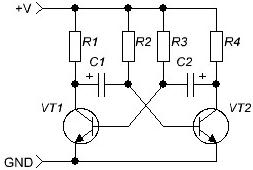
Figura 4
El multivibrador és un amplificador de dues etapes, cobert per comentaris positius. Si les resistències de càrrega del col·leccionista R1 = R4, les resistències de base R2 = R3 són iguals, i els condensadors C1 = C2 són iguals, el multivibrador s’anomena simètric i genera pulsos d’ona quadrada del tipus meandre - la durada del pols és igual a la durada de la pausa.
El cicle de treball d'aquest tipus de polsos (la relació entre el període i la durada del pols) és igual a dos. En els esquemes en anglès, tot és exactament al contrari: en diuen cicle de treball. Es calcula com la relació de la durada del pols al període de la seva successió i s’expressa en percentatge. Així, per al meandre, el cicle de treball és del 50%.
L’ordinador és correcte?
El nom multivibrador va ser proposat pel físic holandès van der Pol, perquè l'espectre d'un senyal rectangular conté molts harmònics. Podeu comprovar-ho si podeu col·locar un receptor de ràdio que funcioni a la gamma d'ona mitjana prop d'un multivibrador que funcioni fins i tot a una freqüència d'àudio: els urls provenen de l'altaveu. Això suggereix que a més de la freqüència sonora, el multivibrador també emet oscil·lacions d'alta freqüència.
Per determinar la freqüència de generació, es pot utilitzar la fórmula f = 700 / (C1 * R2).
Amb aquesta forma de fórmula, la capacitança del condensador en microfarads (μF), la resistència en quilo-ohms (KΩ), el resultat en hertz (Hz). Així, la freqüència està determinada per la constant de temps del circuit C1 * R2; les càrregues del col·lector no afecten la freqüència. Si prenem C1 = 0,02 μF, R2 = 39 KΩ, obtindrem f = 700 / (0,02 * 39) = 897,4 Hz.
Multivibrador en l’era dels ordinadors i microcontroladors Segons aquest esquema, gairebé mai s’utilitza, tot i que pot ser adequat per a diversos experiments. En primer lloc, utilitzant ordinadors. Així sembla el circuit multivibrador muntat al programa Multisim. La connexió de l’oscil·loscopi també es mostra aquí.
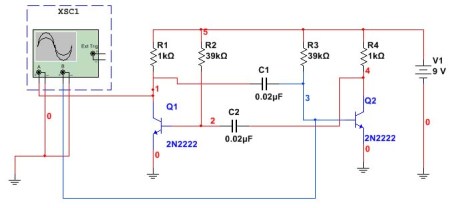
Figura 5
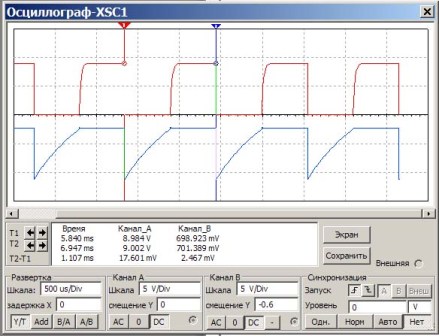
En aquest circuit s’instal·len condensadors i resistències com en l’exemple anterior. La tasca és comprovar el càlcul segons la fórmula si s’obtindrà la mateixa freqüència. Per fer-ho, mesura el període dels polsos i, després, calcula-los en freqüència. La figura 6 mostra el resultat de l’oscil·loscopi Multisim.
Figura 6
Algunes aclariments a la figura 6.
A la pantalla de l’oscil·loscopi, el pols vermell mostra els polsos al col·lector de transistors i el blau a les bases. A sota de la pantalla d'una gran finestra blanca, els números mostren els resultats de la mesura. Ens interessa la columna "Temps". El temps es mesura mitjançant els indicadors T1 i T2 (triangles vermells i blaus per sobre de la pantalla).
Així, el període de repetició del pols T2-T1 = 1.107ms es mostra amb molta precisió. Només queda per calcular la freqüència f = 1 / T = 1 / 1.107 * 1000 = 903Hz.
El resultat és gairebé el mateix que en el càlcul segons la fórmula, que es dóna una mica més alt.
Els condensadors es poden utilitzar no només per separat: en combinació amb resistències, et permeten simplement crear diversos filtres o crear circuits de canvi de fase. Però això es tractarà en el proper article.
Continuació de l'article: Condensadors en circuits electrònics. 2a part
Boris Aladyshkin
Consulteu també a electro-ca.tomathouse.com
: