Categories: Articles destacats » Electricistes novells
Nombre de visualitzacions: 57937
Comentaris sobre l'article: 4
Àlgebra booleana. Part 3. Esquemes de contacte
 L'article descriu els principis bàsics per dissenyar circuits de relé d'acord amb un algoritme determinat del seu funcionament.
L'article descriu els principis bàsics per dissenyar circuits de relé d'acord amb un algoritme determinat del seu funcionament.
En dos articles anteriors se li va parlar dels fonaments bàsics Àlgebra booleana i àlgebra del relé. Sobre aquesta base, es van desenvolupar fórmules estructurals i ja es van desenvolupar circuits de contacte típics.
Elaborar una fórmula estructural segons un esquema ja preparat és senzill. És molt més difícil presentar el circuit elèctric de la futura màquina en la fórmula estructural ja preparada. Necessita una mica de formació!
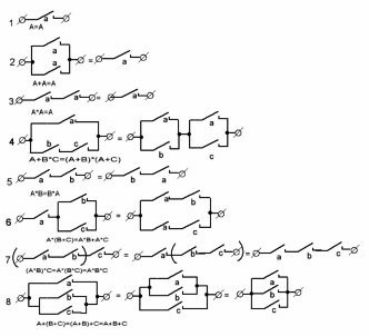
La figura 1 mostra les opcions més habituals. circuits de contacte i els seus equivalents. Ajudaran en la preparació de circuits elèctrics de les màquines, i analitzaran estructures ja preparades, per exemple, durant el procés de reparació.
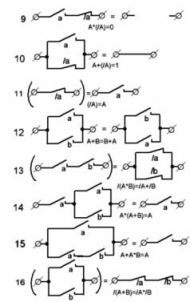
Com podeu utilitzar les opcions per als circuits de contacte comentats anteriorment?
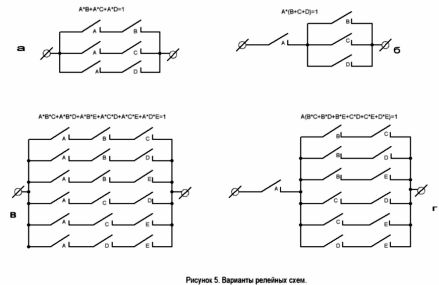
Considereu el circuit que es mostra a la figura 2, a. La fórmula estructural corresponent té la forma: (A + B) * (C + D).
Utilitzant la llei de distribució de l'àlgebra booleana, obrim els claudàtors en aquesta expressió i obtenim: A * (C + D) + B * (C + D), que correspon a l'esquema que es mostra a la figura 2, b. A més, a causa de la multiplicació, podem obtenir la fórmula A * C + A * D + B * C + B * D, corresponent a la figura 2, c.
Els tres esquemes són equivalents, és a dir, resulten tancats en les mateixes condicions. Tanmateix, són diferents en complexitat.
Figura 1. Circuits de contacte típics
El primer dels circuits, el més senzill, requereix quatre relés, cadascun dels quals ha de tenir un contacte normalment obert. (Per simplificar els dibuixos, no es mostren les bobines de relé).
L’esquema “b” requereix un relé amb dos grups de contacte. En realitat, la tasca principal de l’àlgebra dels circuits de contacte és trobar tots els circuits equivalents de manera que pugueu triar el més senzill d’ells.
Figura 2. Circuits de contacte equivalents.
Per consolidar el material tractat, intenteu resoldre tu mateix els problemes següents.
1. Dibuixa el diagrama de circuit d’un autòmat amb la fórmula estructural A * B * C * D + A * B * E + A * D.
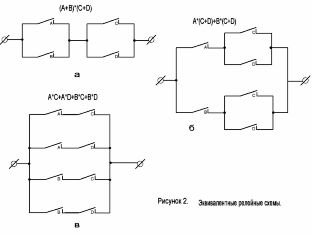
2. Proveu que els circuits que es mostren a la figura 3, a i b, són equivalents.
3. Simplifiqueu el circuit que es mostra a la figura 3, c.
4. Quina fórmula estructural implementa l’esquema de la figura 3, d?
Després del que ja hem estudiat, es podrà començar a resoldre els problemes que es van plantejar al principi del primer article. Els recordem breument.
La primera tasca va ser encendre i apagar la bombeta de l’habitació amb tres interruptors situats en diferents llocs: a la porta, a la taula, al llit.
La segona tasca és votar jutges esportius: de cada quatre jutges “FOR” han de votar almenys dos, sempre que “FOR” el president de la comissió voti.
La tercera tasca era només amb finalitats educatives. Va proposar el mateix que en el primer, només per a sis interruptors, com si hi hagués sis parets a la sala. Circuits similars s’acaben de desenvolupar mitjançant l’àlgebra dels circuits de relé.
En general, si volem desenvolupar un esquema que tingui algunes propietats lògiques donades, podem abordar aquest problema de dues maneres diferents. Convencionalment, aquests camins poden ser anomenats "intuïtius" i "algebraics".
Algunes tasques es resolen millor de la primera manera, mentre que d’altres de la segona. El plantejament intuïtiu resulta més convenient quan el funcionament del circuit està controlat per molts commutadors, però hi ha certa simetria en la disposició mútua d’aquests relés. Veurem que aquí un enfocament intuïtiu condueix a l’objectiu més ràpidament, mentre que l’ús de l’aparell de l’àlgebra del relé en el cas de moltes variables pot ser molt feixuc. És útil conèixer ambdós possibles enfocaments per resoldre aquest problema.
Comencem amb un enfocament intuïtiu. Suposem que necessitàvem construir un circuit tancat quan funcionessin tots els circuits de relé de control.
La solució a aquest problema no necessita una deliberació llarga: és clar que es complirà la condició establerta si interconnectats seqüencialment n contactes de relé normalment oberts.
De la mateixa manera, és obvi que per construir un circuit que es tanqui quan almenys un dels n relés s’ha disparat, és suficient connectar n contactes del relé normalment oberts en paral·lel.
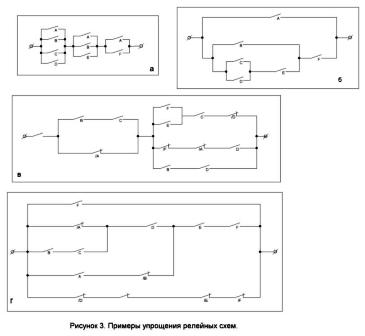
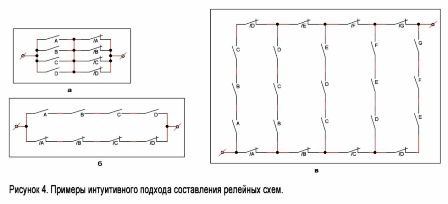
És fàcil imaginar un circuit que es tanqui quan es desencadenen alguns relleus, però no tots. Aquest circuit es mostra a la figura 4, a. A la dreta hi ha un diagrama que funciona amb el principi de "tot o res". Només es tancarà quan es desconnectin tots els relés o es desconnectin (figura 4, 6).
Penseu en un exemple més complex. Que hi hagi n contactes situats en una seqüència específica: A, B, C, D, E, F ... Construirem un circuit que es tanqui quan es tanquen els contactes connectats a la sèrie k i només ho són. Un esquema per als valors n = 7 i k = 3 es mostra a la figura 4, c. En aquesta figura es mostra clar el mètode per a construir aquests esquemes per a qualsevol altre valor de n i k.
Procedim a la construcció de circuits d’acord amb les condicions donades del seu treball mitjançant àlgebra de relé.
Com abans, les condicions de funcionament del circuit sempre s’ajusten de forma verbal. El dissenyador, en primer lloc, ha de ser capaç de posar en paraules allò que vol. Si no té tanta claredat, llavors cap àlgebra ajudarà. Sempre heu de començar amb una declaració clara dels requisits que s’estableixen abans del nou esquema. Com en qualsevol negoci, potser aquesta tasca és la més difícil. Si les condicions són prou senzilles, podem escriure immediatament una expressió d’una fórmula estructural que compleixi aquests requisits.
Exemple 1 Suposem que hem de construir un circuit que contingui 4 contactes A, B, C i D per tal que el circuit s’encengui quan es tanqui el contacte A i un dels altres tres contactes. En aquest cas senzill, el funcionament del circuit per escrit s’assemblarà a aquest aspecte: “El circuit hauria de dur a terme el corrent si es tanquen els contactes A i B, o els contactes A i C o els contactes A i D. Està d’acord que ara és molt senzill elaborar una fórmula estructural. Semblarà així:
A * B + A * C + A * D = 1 o A * (B + C + D) = 1.
El circuit té dues opcions. Es mostren a la figura 5. La segona opció no requereix un relé amb tres contactes normalment oberts.
Exemple 2 El primer article era la tasca número 2 sobre la votació dels jutges esportius. Llegiu més de prop la seva condició, és similar a l’exemple que s’acaba d’examinar. Un registre verbal més clar dels requisits serà aquest: "És necessari elaborar un circuit que contingui 5 contactes A, B, C, D, E, de manera que condueixi el corrent i s'encengui el llum quan es tanquen els contactes següents:
A i B i C, o A i B i D, o A i B i E, o A i C i D, o A i C i E, o A i D i E. El contacte A és el botó del president. Si no es premsa, cadascun dels 6 productes lògics serà 0, és a dir. La votació no va tenir lloc.
La fórmula estructural serà la següent:
(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,
o A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.
Les dues variants del circuit es mostren a la figura 5, c i d. Aquesta és la solució del problema.
Tenint certa habilitat en la lectura de fórmules estructurals, és fàcil imaginar el circuit de l'autòmat en si i totes les seves capacitats. Curiosament, l’àlgebra dels circuits de relé proporciona més informació que fins i tot el propi circuit. Permet veure quants i quins relés es requereixen. Amb la seva ajuda, podeu trobar fàcilment la versió més senzilla de la màquina del circuit.
Exemple 3 Després d’haver adquirit una mica d’experiència en l’elaboració de fórmules estructurals, intentarem resoldre el problema que va començar primer article: heu de dissenyar un interruptor que us permeti encendre la llum en entrar a l'entrada i apagar-la un cop heu pujat al pis desitjat, o, per contra, encendre-la en sortir del pis i apagar-la després de baixar. La mateixa situació succeeix en un llarg passadís: en un extrem s’ha d’encendre la bombeta i, després d’anar a l’altre extrem, extingir-se. En resum, la tasca es redueix a controlar una bombeta de diferents llocs amb dos interruptors.
Escollim el procediment següent per resoldre el problema: primer, formulem clarament les condicions de funcionament dels interruptors, després els escrivim en forma de fórmula i dibuixarem un circuit elèctric utilitzant-los.
Per tant, perquè la bombeta es cremés (1), és necessari que es compleixi una de les dues condicions:
1. Enceneu l’interruptor a la part inferior (A) i desactiveu-lo a la part superior (/ B). Entra al porxo.
2. Enceneu l’interruptor a la part superior (B) i desactiveu la part inferior (/ A).
Utilitzant la notació acceptada, la fórmula estructural s’escriu de la manera següent:
A * (/ B) + (/ A) * B = 1
El diagrama de circuit de l’interruptor es mostra a la figura 6. Actualment, aquests interruptors estan disponibles comercialment, es tracta dels anomenats interruptors d'alimentació. Per tant, la consideració d'aquests esquemes es considera simplement pel concepte dels principis generals del seu treball.
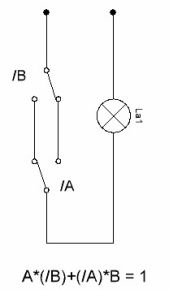
Figura 6
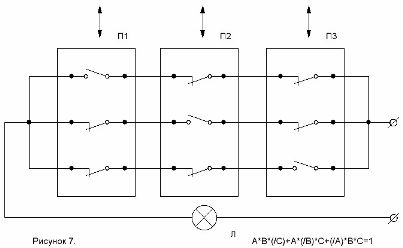
A la tasca número 1 al començament del primer article, parlàvem d’un esquema que permet encendre i apagar la llum de l’habitació amb qualsevol dels tres interruptors. Raonament de la mateixa manera que en el cas de dos interruptors, obtenim la fórmula estructural:
A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.
La figura 7 mostra l'esquema elaborat per aquesta fórmula.
Figura 7
Al començament del primer article, es va proposar una senzilla tasca educativa núm. 2: com si hi hagués sis parets a la sala i cadascuna tenia un interruptor. La lògica del circuit és exactament la mateixa que per als tres commutadors. Denotem-les per les lletres A, B, C, D, E, F. Recordem que la notació (/ A), (/ B) i així successivament, no es tracta d’un signe de divisió, sinó d’una negació lògica. Més sovint indicat per subratllar caràcters i, fins i tot expressions enteres, a la part superior. En alguns esquemes, aquest guió subratllat es substitueix simplement per un signe menys. Per tant, la fórmula estructural dels sis interruptors és:
(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *
(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.
Es convida als lectors a elaborar un circuit elèctric complet que implementi aquesta fórmula estructural per adquirir habilitats pràctiques en el disseny de circuits. Una mica de pista: per al circuit necessitareu sis relés, cadascun dels quals té un contacte normalment obert i cinc normalment tancat. Aquests relleus complexos, si és necessari, es poden muntar des de diversos més simples connectant les seves bobines en paral·lel.
Això conclou la història de l'àlgebra booleana i l'àlgebra dels circuits de relé.
Continuació de l'article: Xips de lògica
Boris Aladyshkin
Consulteu també a electro-ca.tomathouse.com
: