Categories: Electrònica pràctica, Electricistes novells
Nombre de visualitzacions: 77535
Comentaris sobre l'article: 1
Xips de lògica. Part 2: Gates
Els elements lògics funcionen com a elements independents en forma de microcircuits amb un petit grau d’integració i s’inclouen com a components en microcircuits d’un grau d’integració superior. Aquests elements es poden comptar més d’una dotzena.
Però primer, només parlarem de quatre: aquests són els elements I, O, NO i I NO. Els elements principals són els tres primers, i l’element AND-NOT ja és una combinació dels elements AND I NOT. Aquests elements es poden anomenar "maons" de la tecnologia digital. En primer lloc, cal considerar quina és la lògica de la seva acció?
Recordeu la primera part de l'article sobre circuits digitals. Es deia que la tensió a l'entrada (sortida) del microcircuit dins de 0 ... 0,4 V és el nivell de zero lògic o baixa tensió. Si la tensió està dins de 2,4 ... 5,0 V, aquest és el nivell d'una unitat lògica o una tensió d'alt nivell.
L’estat de funcionament dels microcircuits de la sèrie K155 i d’altres microcircuits amb tensió d’alimentació de 5V es caracteritza precisament per aquests nivells. Si la tensió a la sortida del microcircuit està entre 0,4 ... 2,4 V (per exemple, 1,5 o 2,0V), ja podeu pensar en substituir aquest microcircuit.
Consells pràctics: per assegurar-vos que aquest microcircuit és defectuós en la sortida, desconnecteu l’entrada del microcircuit que el segueix (o diverses entrades connectades a la sortida d’aquest microcircuit) d’aquest. Aquestes entrades poden simplement “assentar” (sobrecarregar) el xip de sortida.
Convencions gràfiques
Els símbols gràfics són un rectangle que conté línies d’entrada i sortida. Les línies d’entrada dels elements es troben a l’esquerra i les línies de sortida a la dreta. El mateix s’aplica als fulls sencers amb circuits: a la part esquerra s’introdueixen tots els senyals, a la dreta hi ha sortides. És com una línia d'un llibre, que serà més fàcil de recordar d'esquerra a dreta. A l'interior del rectangle hi ha un símbol condicional que denota la funció que realitza l'element.
Element lògic AND
Comencem la consideració d’elements lògics amb l’element I.
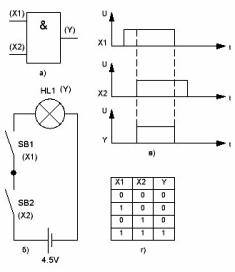
Figura 1. L’element lògic AND
La seva designació gràfica es mostra a la figura 1a. El símbol de la funció And és el símbol anglès "&", que en anglès substitueix la unió "i", perquè al capdavall, tota aquesta "pseudociencia" es va inventar a la maleïda burgesia.
Les entrades de l’element es designen com X amb els índexs 1 i 2, i la sortida, com a funció de sortida, per la lletra Y. És senzilla, com en matemàtiques escolars, per exemple, Y = K * X o, en el cas general, Y = f (x). Un element pot tenir més de dues entrades, que només es limita a la complexitat del problema que es resol, però només hi pot haver una sortida.
La lògica de l’element és la següent: un voltatge d’alt nivell a la sortida Y serà només quan I a l’entrada X1 I a l’entrada X2 hi haurà una tensió d’alt nivell. Si l’element té 4 o 8 entrades, aleshores s’ha de satisfer la condició indicada (nivell alt) a totes les entrades: I-a l’entrada 1, I-a l’entrada 2, I-a l’entrada 3 ... .. I -a l’entrada N. Només en aquest cas, la sortida també serà d’un nivell elevat.
Per tal de facilitar la comprensió de la lògica del funcionament de l'element And, es mostra el seu analògic en forma de circuit de contacte a la figura 1b. Aquí, la sortida de l’element Y és representada per la làmpada HL1. Si la làmpada està encesa, això correspon a un nivell alt a la sortida de l’element I. Sovint aquests elements s’anomenen 2-I, 3-I, 4-I, 8-I. El primer dígit indica el nombre d’entrades.
Com a senyals d'entrada X1 i X2, s'utilitzen botons ordinaris de "campana" sense corregir. L’estat obert dels botons és un estat de nivell baix, i l’estat tancat és naturalment alt. Com a font d’energia, el diagrama mostra una pila galvànica. Mentre els botons estan en estat obert, la làmpada, per descomptat, no s’encén. La làmpada només s’encén quan es prem dos botons alhora, és a dir. I-SB1, I-SB2.Aquesta és la connexió lògica entre el senyal d'entrada i sortida de l'element I.
Es pot obtenir una representació visual del funcionament de l’element AND mirant el diagrama de temps que es mostra a la figura 1c. Al principi, apareix un senyal d’alt nivell a l’entrada X1, però a la sortida Y no va passar res, encara hi ha un senyal de baix nivell. A l’entrada X2, el senyal apareix amb cert retard respecte a la primera entrada i apareix un senyal d’alt nivell a la sortida Y.
Quan el senyal a l’entrada X1 és baix, la sortida també s’estableix a baixa. O, dit d'una altra manera, es manté un senyal d'alt nivell a la sortida sempre que hi hagi senyals d'alt nivell a les dues entrades. El mateix es pot dir dels elements més multi-entrada de I: si és 8-I, llavors per obtenir un nivell alt a la sortida, s’ha de mantenir el nivell alt a les vuit entrades alhora.
La majoria de vegades a la literatura de referència, l’estat de la sortida d’elements lògics en funció dels senyals d’entrada es dóna en forma de taules de veritat. Per a l’element considerat 2-I, la taula de veritat es mostra a la figura 1d.
La taula és una mica similar a la taula de multiplicació, només més petita. Si ho estudieu detingudament, notareu que un nivell alt a la sortida serà només quan hi ha una tensió d’alt nivell o, el que és el mateix, hi ha una unitat lògica a les dues entrades. Per cert, la comparació de la taula de veritat amb la taula de multiplicacions no és gaire casual: totes les taules de veritat de l'electrònica ho saben, com diuen, de cop.
També, es pot descriure amb la funció I àlgebra de lògica o àlgebra booleana. Per a un element de dues entrades, la fórmula serà així: Y = X1 * X2 o una altra forma d'escriure Y = X1 ^ X2.
Element lògic OR
A continuació mirarem la porta O.
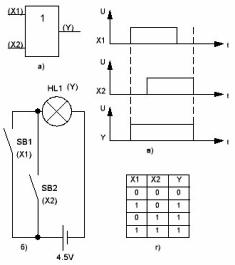
Figura 2. OR de porta lògica
La seva designació gràfica és similar a l’element AND que s’acaba d’examinar, tret que en lloc del símbol & per a la funció AND, el número 1 s’inscrigui dins del rectangle, tal com es mostra a la figura 2a. En aquest cas, denota la funció OR. A l'esquerra hi ha les entrades X1 i X2, que, com en el cas de la funció And, poden ser més, i a la dreta, la sortida, indicada per la lletra Y.
En forma d’una fórmula d’àlgebra booleana, la funció O s’escriu com a Y = X1 + X2.
D’acord amb aquesta fórmula, Y serà cert quan OR a l’entrada X1, O a l’entrada X2, O a les dues entrades hi haurà immediatament un nivell alt.
El diagrama de contactes que es mostra a la figura 2b ajudarà a comprendre el que s’acaba de dir: si premeu qualsevol dels botons (nivell alt) o tots dos botons alhora, la llum llueix (nivell alt). En aquest cas, els botons són els senyals d’entrada X1 i X2, i la llum és el senyal de sortida Y. Per facilitar el record, les figures 2c i 2d mostren el diagrama de cronometratge i la taula de veritat, respectivament: n’hi ha prou amb analitzar el funcionament del circuit de contacte mostrat amb el diagrama i la taula, com totes les preguntes. desapareixerà.
Element lògic NO, inversor
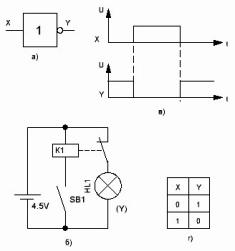
Com va dir un professor, a la tecnologia digital no hi ha res més complicat que un inversor. Potser això és de fet.
En l'àlgebra de la lògica, l'operació NO s'anomena inversió, que significa negació en anglès, és a dir, el nivell del senyal a la sortida correspon exactament al contrari al senyal d'entrada, que sembla Y = / X en forma de fórmula.
(La barra abans de X denota la inversió real. Normalment, el guió baix s'utilitza en lloc de la barra, encara que aquesta notació és força acceptable.)
El símbol gràfic de l'element NO és un quadrat o rectangle en el que s'inscriu el número 1.
Figura 3. Inverter
En aquest cas, vol dir que aquest element és un inversor. Només té una entrada X i la sortida Y. La línia de sortida comença amb un petit cercle, que indica que aquest element és un inversor.
Com acabem de dir, un inversor és el circuit digital més complex.I ho confirma el seu esquema de contactes: si abans només n’hi havia prou amb els botons, ara se’ls ha afegit un relé. Tot i que no es prem el botó SB1 (zero lògic a l’entrada), el relé K1 es desactiva i els contactes normalment tancats activen la bombeta HL1, que correspon a una unitat lògica a la sortida.
Si premeu el botó (apliqueu una unitat lògica a l’entrada), el relé s’encendrà, s’obriran els contactes K1.1, s’apagarà la llum, que correspon a un zero lògic a la sortida. A continuació es confirma el diagrama de temps de la figura 3c i la taula de veritat de la figura 3d.
Element lògic I NO
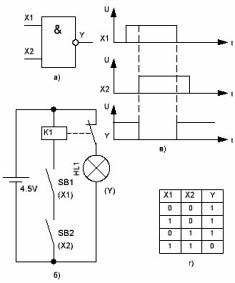
La porta AND NO és una combinació de la porta AND i la porta NOT.
Figura 4. L’element lògic I NO
Per tant, el símbol & (lògic AND) està present al seu símbol gràfic, i la línia de sortida comença amb un cercle que indica la presència d’un inversor a la composició.
L’analogic de contacte de l’element lògic es mostra a la figura 4b i, si us fixeu bé, és molt similar a l’anàleg de l’inversor mostrat a la figura 3b: la bombeta també s’encén a través dels contactes normalment tancats del relé K1. En realitat aquest és l’inversor. El relé està controlat pels botons SB1 i SB2, que corresponen a les entrades X1 i X2 de la porta AND. El diagrama mostra que el relé només s’encendrà quan es prem els dos botons: en aquest cas, els botons realitzen la funció & (lògic AND). En aquest cas, la làmpada a la sortida s’apaga, que correspon a l’estat de zero lògic.
Si no es premeu els dos botons, o almenys un d’ells, el relé està desactivat i la llum de la sortida del circuit està encesa, que correspon al nivell d’una unitat lògica.
A partir de l'anterior, podem treure les conclusions següents:
En primer lloc, si almenys una entrada té un zero lògic, la sortida serà una unitat lògica. El mateix estat a la sortida serà el cas en què hi hagi zeros a les dues entrades alhora. Aquesta és una propietat molt valuosa d’elements AND-NOT: si connecteu les dues entrades, l’element AND-NOT es converteix en inversor: només fa la funció de NOT. Aquesta propietat permet no posar un xip especial que conté sis inversors alhora, quan només calen un o dos.
En segon lloc, zero a la sortida només es pot obtenir si es "recopila" a totes les entrades d’unitat. En aquest cas, convindria anomenar l’element lògic considerat 2I-NOT. Els dos diuen que aquest element és de dues entrades. A gairebé totes les sèries de microcircuits també hi ha elements de 3, 4 i vuit entrades. A més, cadascun d'ells només té una sortida. Tanmateix, l’element 2I-NOT es considera un element bàsic en moltes sèries de microcircuits digitals.
Amb diverses opcions per connectar les entrades, podeu obtenir una altra propietat meravellosa. Per exemple, connectant les tres entrades de l’element de vuit entrades 8I-NOT junts, obtenim l’element 6I-NOT. I si connecteu totes les 8 entrades junts, obteniu només un inversor, com s'ha esmentat anteriorment.
Això completa la coneixença amb els elements lògics. A la propera part de l’article, considerarem els experiments més senzills amb microcircuits, l’estructura interna de microcircuits, dispositius senzills, com ara generadors d’impulsos.
Boris Aladyshkin
Continuació de l'article: Xips de lògica. 3ª part
Consulteu també a electro-ca.tomathouse.com
: