Àlgebra booleana. Part 2. Lleis bàsiques i funcions

Continuació de la història sobre l'àlgebra booleana, convencions, regles, operacions. Transició als conceptes bàsics dels circuits de contacte.

Dins primer article George Bull va ser descrit com el creador de l'àlgebra de la lògica. El segon article descriurà les operacions bàsiques de l'àlgebra booleana i els mètodes per simplificar les expressions booleanes. Així doncs, l'àlgebra booleana utilitza les afirmacions com a arguments, i no el seu significat, sinó la veritat o la falsedat de l'afirmació.

La forma per escriure expressions en àlgebra booleana.

Si l’afirmació és certa, s’escriu així: A = 1, si és falsa, aleshores A = 0 (al cap i a la fi, no és cert que la patata sigui una fruita). Per a qualsevol afirmació, A és cert (A = 1) o fals (A = 0). Aquí no hi pot haver cap mitjà. Ja hem parlat d’això.

Si connecteu dues instruccions senzilles amb la unió I, obteniu una declaració complexa, que s’anomena producte lògic. Prenguem dos refranys simples: “Tres és més que dos” designarem per la lletra A, “Tres menys de cinc” - per la lletra B.

D’aquí que la complexa afirmació “Tres és més de dos i menys de cinc” és lògica (en aquest cas, majúscula I, diu que es tracta d’una operació lògica “I”, així com més endavant en els textos “O” i “NO”). i B. Es designa així: A ^ B o A * B.

Multiplicació lògica (operació "I").

En àlgebra elemental A * A = A2. Però en l'àlgebra de Buhl, A * A = A2 = A, A * A = A ja que el signe de multiplicació (*) ara significa ... I ... en el sentit de I ... I. Tota la nostra experiència confirma que A&A és el mateix que A., no es pot discrepar. La veritat de l’afirmació no canvia si es repeteix el factor diverses vegades.

El producte de dues afirmacions es considera veritable (igual a 1), doncs, i només si tots dos factors són certs, i fals (igual a 0) si almenys un dels factors és fals. D’acord que aquestes regles no contradiuen el sentit comú i, a més, compleixen plenament les regles de l’àlgebra elemental:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

La primera igualtat diu el següent: si tant A com B són certes, el producte A * B és cert. A l'àlgebra Buhl, el signe de multiplicació (*) substitueix la unió I.

Els productes lògics poden incloure no dos, però un nombre més gran de declaracions. I en aquest cas, el producte només és cert quan alhora tots els enunciats-factors són certs.

Addició lògica (operació O)

Si dues declaracions estan connectades per una unió OR. que l'oració composta formada s'anomena suma lògica.

Considereu un exemple de suma lògica. Dient A: "Avui aniré al cinema".

Declaració B: "Avui aniré a la discoteca". Afegim les dues declaracions i aconseguim: "Avui aniré al cinema O a una discoteca".

Aquesta afirmació complexa es denota de la manera següent: A + B = C o (A V B) = C.

Per C vam desmentir una declaració complexa d’una suma lògica.

En l'exemple que es considera, la unió O no es pot utilitzar en un sentit exclusiu. De fet, el mateix dia podeu arribar al cinema i a la discoteca. I aquí està la dita:

"El president de l'associació de jardineria serà Petrov o Ivanov" - no és una suma lògica, perquè només una persona serà el president i l'altre serà un jardiner aficionat ordinari.

El signe V per a la suma lògica es tria perquè és la lletra inicial de la paraula llatina "vel", que significa "o", en contrast amb la paraula llatina "aut>, que significa" i ". Ara hauria de quedar clar per a tothom per què el producte lògic s’indica amb el signe ^.

A l'àlgebra elemental hi ha una regla A + A = 2A. Aquesta regla és certa, independentment de quin nombre sigui representat per la lletra A. En l'àlgebra booleana, la regla A + A = A. li correspon.

Com qualsevol afirmació composta, la suma de les dues afirmacions A i B pot ser certa o falsa. La suma es considera certa, és a dir, igual a la unitat, si almenys un dels termes és cert:

A + B = 1 si OR A = 1 O B = 1, que és coherent amb l'aritmètica convencional:

1+0 = 0+1 = 1.

Si ambdues afirmacions sumades són certes, la suma també es considera certa, per tant, en l'àlgebra booleana tenim: (1) + (1) = 1.

Els claudàtors s'estableixen aquí per tal de subratllar el condicional, el significat d'aquesta addició i no l'aritmètica.

La suma de dues afirmacions es considera falsa i és igual a zero si, però només si els dos termes són falsos. A partir d’aquí:

0 + 0=0.

Per tant, la suma de les dues afirmacions A + B es considera certa si és certa, O, A, O B, O tots dos termes junts. Així, la paraula OR es designa amb +.

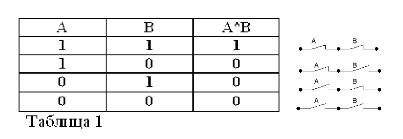
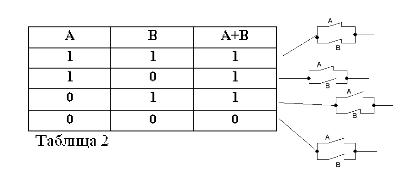
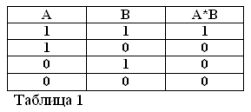
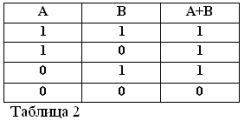
Recordant que les afirmacions A i B només poden ser certes o falses i, per tant, tenir una mesura de veritat 1 o 0, els resultats de les operacions AND i OR considerades es poden resumir en les taules 1 i 2.

La tercera operació, àmpliament utilitzada per l'àlgebra Buhl, és l'operació de negació - NO. El recordem que l'àlgebra elemental utilitza les operacions ADD, D Resta, Multiplica per, Divideix per, i algunes altres.

Per a cada afirmació A, hi ha la seva negació NO A, que notarem pel símbol / A. Això no hauria de ser de dubte.

Donem exemples: “Anirem al bosc” A, “No anirem al bosc” / A.

Si l’afirmació A és certa, és a dir, A = 1, la seva negació / A ha de ser falsa / A = 0. I viceversa, si alguna afirmació és falsa, la seva negació és certa. Per exemple: "Un cavall no menja fenc" / A = 0, "Un cavall no menja fenc" (A = 1). Això es pot expressar a la taula 3.

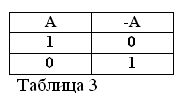
Determinar el significat de l’acció de negació i assumir que de les dues afirmacions A i / A sempre és una veritat, segueixen dues fórmules noves de l’àlgebra booleana:

A + (/ A) = 1 i A * (/ A) = 0.

També hi ha altres fórmules que simplifiquen el processament lògic d’enunciats. Per exemple, 1 + A = 1, ja que, segons la definició d’addició, en el cas que un terme sigui igual a unitat, la suma sempre és igual a unitat. El resultat obtingut no depèn de si A = 0 o A = 1.

Cadascuna de les tres operacions lògiques que examinem (AND, O, NO) té unes propietats que s’aproximen a les regles de l’àlgebra elemental. Si es formulen tots, obtenim 25 regles de l'àlgebra booleana. Són prou per resoldre gairebé qualsevol problema lògic. Sense aquestes regles, es fa força difícil resoldre problemes lògics per la seva aparent complexitat. Intentar trobar la resposta correcta sense utilitzar les regles significa substituir-les per enginy i raonaments generals. Les normes faciliten molt aquest treball i estalvien temps.

En el marc de l’article és impossible tenir en compte totes aquestes 25 regles, però qui ho desitgi sempre les pot trobar a la literatura pertinent.

Com ja s’ha esmentat en el primer article del 1938, el jove científic nord-americà Claude Shannon al seu article “Anàlisi simbòlica dels relés i commutació de circuits” per primera vegada utilitza àlgebra booleana per a problemes de tecnologia de relé. El descobriment de Shannon va ser que es va adonar que el mètode per dissenyar màquines de relé i ordinadors electrònics és en realitat una branca de la lògica matemàtica.

Sovint passa. Durant molts anys, el científic treballa en un problema que sembla completament innecessari per als seus compatriotes: només divertit. Però passen dècades i, de vegades, segles, i una teoria que ningú necessita no només adquireix el dret a existir, sinó que sense ella s’avança un creixement més avancable.

Què va ajudar a Shannon per segona vegada a "descobrir" l'àlgebra booleana? Cas? Res del tipus.

L’amor a les màquines de relé, construïdes en interruptors i relés convencionals, va ajudar el jove científic a connectar una teoria oblidada amb les tasques de les centrals telefòniques automàtiques, en què treballava aleshores. Posteriorment, Shannon va introduir la mateixa idea del "sí o no" en missatges discrets i va posar les bases de tota una secció de cibernètica: teoria de la informació.

L’àlgebra de Buhl era molt adequada per a l’anàlisi i la síntesi de circuits de relé. N’hi havia prou d’acceptar com a veritable afirmació: “Hi ha un senyal al circuit”, i com a falsa: “No hi ha cap senyal al circuit”, ja que apareixia una nova àlgebra: l’àlgebra del senyal, l’àlgebra del circuit de relé.

La nova àlgebra només és vàlida per a la consideració de circuits de relé i commutació. Al cap ia la fi, només en aquests esquemes es compleix la condició "hi ha un senyal" i "cap senyal". Quan el senyal canvia contínuament, adquirint un nombre arbitràriament gran de condicions intermèdies (un senyal s'anomena analògic), l'àlgebra del relé no és aplicable. Això sempre s’ha de recordar. Però només la majoria d’ordinadors electrònics i màquines cibernètiques utilitzen el principi discret de processament de senyal, que es basa en els elements “sí - no”.

Shannon va acceptar l'expressió "Contacte tancat" com a veritable (1), i "Contacte obert" com a falsa (0). La resta de "l'àlgebra", incloses les operacions AND, OR i NO i 25 regles, Shannon va manllevar a Boole.

L’àlgebra del circuit de relé va resultar ser més simple que l’àlgebra booleana, ja que només tracta d’elements del tipus “sí - no”. A més, la nova àlgebra és més visual.

Els elements d’aquesta àlgebra són els contactes, que denotarem amb les lletres A, B, C ... El contacte està tancat - A, el contacte està obert - / A (lletra amb traç).

Com veieu, la notació està extreta de l'àlgebra booleana. Un contacte obert és la negació d’un contacte tancat. El mateix contacte no es pot tancar ni obrir.

Estem d’acord que si en qualsevol circuit dos contactes es denoten per la mateixa lletra, això vol dir que sempre prenen els mateixos valors.

En un moment donat, tots dos estan oberts alhora, o bé tots dos estan tancats. La manera més senzilla d’imaginar-los connectats mecànicament de manera que tots dos s’obrin o tanquin simultàniament.

Si en alguna cadena un contacte és una negació d’un altre contacte, els seus significats sempre són oposats. Per exemple, els contactes C i / C mai no es poden obrir ni tancar simultàniament. I al diagrama es poden representar connectats mecànicament: si un d’ells s’obre, l’altre es tanca.

Comencem el nostre coneixement amb l'àlgebra del relé analitzant els circuits més senzills que corresponen a les operacions AND, O i NO.

El producte de dos contactes (operació AND) és el circuit obtingut com a resultat de la connexió en sèrie: es tanca (igual a 1) només quan es tanquen els dos contactes (iguals a 1).

La suma de dos contactes (operació O) serà el circuit format quan es connecten en paral·lel: es tanca (igual a 1) quan es tanca almenys un dels contactes que formen el circuit (igual a 1).

El contrari d’aquest contacte (operació NO) és un contacte igual a 0 (obert) si aquest contacte és 1 (tancat) i viceversa.

Com en l'àlgebra booleana, si els contactes es denoten amb les lletres A i B, es denotarà el producte de dos contactes per A * B, la suma per A + B, i el contacte oposat a A, per / A. L'esmentat anteriorment s'explica a les figures 1, 2 i 3.

Validesa de les taules corresponents a les operacions AND, OR i NO. ara ningú no hauria de tenir dubtes.

Posem en dos exemples: 1 * 0 = 0 i 1 + 0 = 1.

La figura es pot veure que un contacte tancat permanentment connectat en sèrie amb un contacte obert constantment equival a un contacte permanentment obert (1 * 0 = 0) Un contacte tancat permanentment connectat en paral·lel amb un contacte obert constantment equival a un contacte tancat permanentment.

Després d'haver-vos familiaritzat amb l'aritmètica dels circuits de contacte, podeu descriure qualsevol circuit de relé amb una fórmula mitjançant les convencions acceptades. En la cibernètica, aquestes fórmules s’anomenen estructurals.

Si la fórmula estructural de qualsevol circuit de relé és 1, llavors hi pot passar un senyal: el circuit està tancat. Per contra, si la fórmula estructural del circuit és 0, el senyal no hi passarà: el circuit es trenca.Conclusió: dos circuits de relé són equivalents entre si quan les seves fórmules estructurals són iguals.

En la continuació de l'article, considerarem exemples de circuits de contacte, circuits de contacte típics i els seus equivalents, així com l'elaboració de diagrames segons fórmules estructurals. També considerem els circuits lògics principals que realitzen les funcions de l'àlgebra booleana.

Continuació de l'article: Àlgebra booleana. Part 3. Esquemes de contacte

Boris Aladyshkin

Comments

[#1 Àlex]

Gràcies

Un punt, paràgraf:

"Com en l'àlgebra booleana, si els contactes es denoten amb les lletres A i B, es denotarà el producte de dos contactes per A * B, la suma per A + B, i el contacte oposat a A, per / A. L'esmentat anteriorment s'explica a les figures 1, 2 i 3 ..."

On es troba la figura 3?