Àlgebra booleana. Part 1. Una mica d’història

A l'escola, tots estudiem l'àlgebra, però allà no parlaven d'algebra booleana. Quina és la diferència entre l'àlgebra booleana i l'àlgebra escolar, la història de la seva aparença, problemes i aplicacions es descriuen en aquest article.

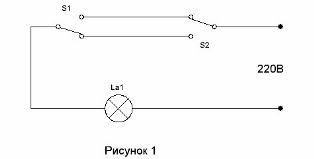
El circuit que permet que dos interruptors s’encenguin la llum al passadís en entrar al passadís i s’apagin en entrar a l’habitació s’ha conegut des de fa molt de temps (vegeu. Circuit de control d’il·luminació de corredor) Es mostra a la figura 1.

Tasca número 1. Més complicat. Creeu un diagrama que us permeti encendre i apagar la llum de la vostra habitació amb qualsevol dels tres interruptors diferents. Els interruptors es troben a l'entrada de l'habitació, a sobre del llit i a l'escriptori.

Tasca número 2.

En un comitè d’esports, com un comitè de fàbrica, es van reunir 5 jutges.

Cadascun d’ells ha de votar per decisions diferents. La decisió s’adopta per majoria de vots, però només amb la condició addicional que el president de la comissió voti a favor.

Els jutges voten prement el botó que tanca l’interruptor situat sota la taula en què s’asseuen. Tancant el commutador, voten a favor, desconnectant els contres. Dibuixa un esquema senzill que et permeti veure automàticament els resultats de la votació. En el cas més senzill, simplement amb l'ajuda d'una bombeta - encesa - la decisió es va prendre, no es va il·luminar - no.

Tasca número 3. A la pràctica, això és poc probable, però com una tasca educativa complexa és força adequada.

A una gran sala hexagonal, hi ha instal·lat un interruptor a cada paret. Creeu un circuit de manera que en qualsevol moment pugueu encendre o apagar la llum de l'habitació girant un (qualsevol) interruptor.

Després d'assegurar-vos sense èxit sobre les tasques de tres a quatre dies, deixeu-les de forma temporal. I emprenyat Àlgebra booleana. És l'àlgebra booleana, o, com també es diu, Àlgebra booleana, àlgebra del circuit de relé, us ajudarà a resoldre els vostres problemes.

Què és l'àlgebra booleana?

Curiosament, malgrat que durant cinc anys porten estudiant l'àlgebra a l'escola, molts estudiants, i més tard adults, no podran respondre la pregunta, què és l'àlgebra? L’àlgebra és una ciència que estudia els conjunts d’alguns elements i les accions sobre ells.

En un curs escolar en àlgebra, aquests elements són nombres. Els nombres es poden denotar no per nombres, sinó per lletres, tothom està familiaritzat amb això. A les primeres lliçons d’àlgebra, això sempre dificulta a molts estudiants. Recordeu el difícil que era al principi acostumar-se a afegir lletres en lloc de números, resoldre equacions que no diuen res.

Probablement, cadascun de nosaltres es va plantejar la nostra pregunta: "Per què necessitem introduir lletres en lloc de números i és necessari en absolut?" I només més tard es va veure quins avantatges dóna l’àlgebra en resoldre problemes en comparació amb l’aritmètica.

L’àlgebra s’utilitza en moltes ciències exactes. Es tracta de física, mecànica, sopromat, electricitat. Llei d'Ohm no hi ha res més que una equació algebraica: n’hi ha prou amb substituir els seus valors numèrics en lloc de lletres per saber quina corrent fluirà en la càrrega o quina resistència té una secció del circuit.

De manera que vau familiaritzar-vos amb l'àlgebra dels nombres o amb l'àlgebra elemental. La principal i gairebé única tasca és obtenir una resposta a la pregunta: “En què és X? Quant? ”

A la secundària estudien els inicis de l'àlgebra vectorial. Aquesta àlgebra és fonamentalment diferent de l'àlgebra elemental. Té una naturalesa diferent del conjunt estudiat i d’altres regles d’actuació. Solucionant l'equació vectorial, obtenim en la resposta un vector que no és un nombre normal que respon a la pregunta "Quant?"

Les fórmules de l'àlgebra vectorial són, en molts aspectes, diferents de les fórmules de l'àlgebra elemental. Per exemple, en l'àlgebra elemental i en l'àlgebra vectorial hi ha una operació d'addició. Però es realitza de maneres completament diferents.L'addició de nombres no és en absolut la suma de vectors.

Hi ha altres àlgebres: àlgebra lineal, àlgebra d’estructures, àlgebra d’anells, àlgebra de lògica o, el que és el mateix, àlgebra booleana. Probablement no heu sentit el nom a les lliçons de l'escola. George Boole - però tothom coneix el nom d’una de les seves talentoses filles Ethel Voinich (1864 - 1960). Va escriure la novel·la "Gadfly", que parla de la lluita pels drets dels carbonaris italians.

George Bull va néixer a Anglaterra el 2 de novembre de 1815. Tota la seva vida va treballar com a professor de matemàtiques i física a l'escola. A partir de les memòries dels seus estudiants se sap quina importància té Bul en el desenvolupament de les habilitats creatives dels estudiants. Al presentar nou material, va voler assegurar que els seus propis estudiants “redescobrissin” algunes fórmules i lleis.

Al estudiant, parlant de les dificultats que els científics van inevitablement afrontar en la cerca de la veritat, el professor li agradava repetir una saviesa oriental: fins i tot el tron ​​persa no pot aportar tant de plaer a una persona com el més petit descobriment científic. Buhl mai va perdre l’esperança que algun dia els seus estudiants fessin un autèntic descobriment.

El ventall d’interessos científics de Buhl era molt ampli: li interessava igualment les matemàtiques i la lògica, la ciència de les lleis i les formes de pensament. En aquells dies, la lògica era considerada una ciència humanitària, i molts que coneixien George Boole es van quedar bocabadats de com els mètodes exactes de cognició inherents a les matemàtiques i els mètodes purament descriptius de la lògica podrien coexistir en una sola persona.

Però el científic volia fer que la ciència de les lleis i de les formes de pensament fos tan estricta com qualsevol de les ciències naturals, diguessin matemàtiques i física. Per fer-ho, Boule va començar a denominar no nombres com a lletres, com es fa en l'àlgebra ordinària, però en afirmacions i va mostrar que aquestes equacions, molt similars a les algebraiques, poden resoldre preguntes sobre la veritat i la falsedat de les declaracions de l'home. Així va sorgir l’àlgebra booleana.

Però molt abans que George Boole, el matemàtic i filòsof alemany Gottfried Leibniz (1646-1716) expressés per primer cop la idea de crear una ciència que designés tots els conceptes del discurs col·loquial ordinari amb símbols i establís una àlgebra nova per combinar aquests símbols.

Després de la creació d’una tal ciència, segons Leibniz, científics i filòsofs deixaran de discutir-se i de cridar-se els uns als altres, esbrinant la veritat, però agafaran un llapis i diuen amb calma: “Calculem!”

Avui, l’àlgebra de la lògica s’ha convertit en una part important de les matemàtiques. Una de les seves tasques és resoldre tot tipus d'equacions, les proporcions numèriques de les quals són substituïdes per alfabètiques. Probablement, cadascun de vosaltres, al llarg de la vostra vida, vau recordar com resoldre equacions de segon i tercer grau amb coeficients de lletra. Així doncs, Boole en la seva nova àlgebra va utilitzar totes aquestes fórmules i regles.

El que és nou en l'àlgebra booleana és que els elements del conjunt que s'hi estudien no són nombres, sinó sentències. Si, quan es resolen equacions algebraiques ordinàries, es determina quin nombre és igual a X desconegut, l'àlgebra escolar busca la resposta a la pregunta: "Quant?"

L’àlgebra de la lògica busca la resposta a la pregunta: “És certa o aquesta afirmació denotada per la lletra X?”

El significat i el contingut de l’enunciat no tenen cap paper aquí. Cada afirmació només pot ser certa o falsa. No pot ser mig veritat i mig fals. A tall d’exemple, podem recordar tirar lots amb una moneda.

Només es consideren dos estats de moneda: els caps o les cues. Per acord de les parts, l'àguila és SÍ, i les cues són NO. En la teoria de probabilitats no es tenen en compte altres punts intermedis, encara que siguin possibles. Una moneda abatible pot caure en un cantell, rodar pel terra fins a les potes d’una cadira o taula i mantenir-se en posició vertical, o fins i tot caure en un ampli buit al terra. (Per analogia amb circuits elèctrics, les dues darreres situacions es poden considerar com un mal funcionament en forma de contacte cremat).Però, en aquells dies, l'àlgebra booleana, per desgràcia, no era gaire utilitzada.

Claude Shannon "va descobrir" l'àlgebra Buhl de nou. El 1938, encara estudiant a l’Institut Tecnològic i Amèrica del Massachusetts, el jove Claude va demostrar que l’àlgebra booleana és perfectament adequada per a l’anàlisi i la síntesi de relés i circuits de commutació.

Amb l'ajuda de l'àlgebra booleana, és molt fàcil fer un circuit elèctric d'un autòmat que funcioni sobre un relé.Per això, només cal saber exactament què ha de fer la màquina, és a dir, cal tenir un algorisme per al seu funcionament. Així doncs, es va establir la base de la teoria de les màquines digitals que funcionen amb el principi de SÍ o NO.

Aquesta és, en resum, la història de l'àlgebra booleana. En els articles següents considerarem les seves lleis bàsiques, exemples de circuits de contacte que implementen aquestes lleis. Considereu la solució d'aquestes tasques que es van donar al començament de l'article.

Continuació de l'article: Àlgebra booleana. Part 2. Lleis bàsiques i funcions

Boris Aladyshkin