Quina és la connexió entre les seccions de filferro i la població de conill?

El 1202, el matemàtic italià Leonardo Fibonacci va publicar el seu treball sota el títol "Llibre d'Abacus" ("Llibre dels càlculs"), en el qual també va descriure les sèries de números immortalitzades pel seu nom. En un dels capítols, Fibonacci intenta mostrar matemàticament com augmentarà el nombre de conills. Va considerar com a condicions les següents hipòtesis:

1) els dos primers mesos un parell de conills no dóna descendència;

2) a partir del tercer mes, un parell de conills dóna un altre parell de conills.

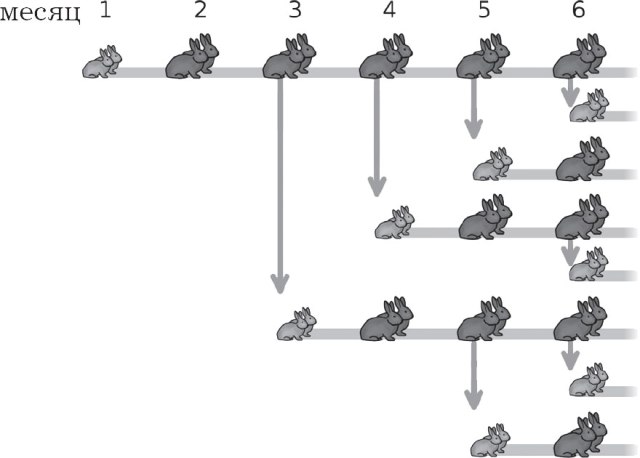
Com a resultat de construir un patró de creixement de la població de conills, obtenim la següent sèrie de números, destacant l’augment del nombre de conills cada mes:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

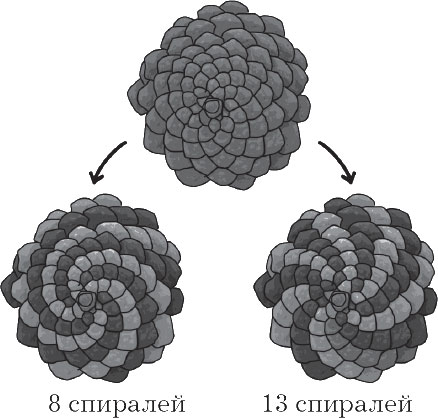
Si mireu detingudament el rebombori, veureu que la seva superfície consisteix en escales que es torcen en espiral d'acord amb la seqüència de Fibonacci. Mentre es troben en una pinya o en una flor de gira-sol, són visibles a simple vista.

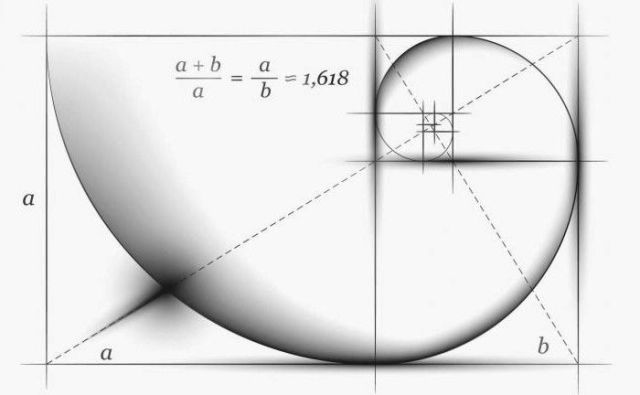
Des de l’època de l’Antiguitat de la Ràtio d’Or, el nombre = 1,618. Els grecs antics consideraven el valor de la proporció ideal. La relació daurada és la relació de cada nombre posterior de la sèrie Fibonacci amb l'anterior:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

Els grecs antics l’utilitzaven en l’arquitectura. La façana del Partenó d'Atenes té proporcions molt similars amb un rectangle construït sobre el principi de la proporció daurada.

Quina és la bellesa de la seqüència de seccions de filferro, els corrents nominals de corrents elèctrics i de tall dels interruptors de circuit? Creeu una sèrie de números amb els valors següents: 1,5; 2,5; 4; 6; 10; 16; 25; 40; 63...

Corrents nominals d’entrants electromagnètics:

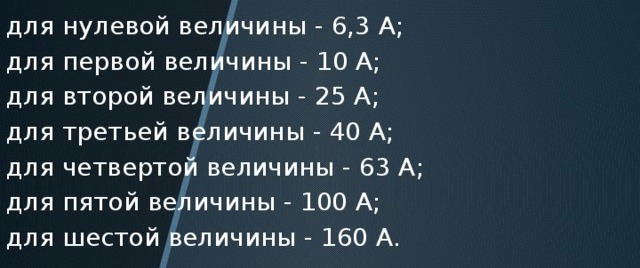
Així, si es divideix 2,5 / 1,5; 4 / 2,5; 6,3 / 4; 10 / 6,3; 16/10; 25/16; 40/25; 63/40llavors obtenim uns 1,6. La qual cosa correspon a la regla de la proporció daurada. I reflecteix la bellesa i el geni de la natura fins i tot en els nostres avorrits sistemes d’enginyeria.

Què en penses? És un accident?

Basat en el llibre "Una gran novel·la sobre matemàtiques. Història del món mitjançant el prisma de les matemàtiques" de Michael Lone. Gràcies per la recomanació de Vladimir Kisel.

Alexey Bushnyaga