"Tot flueix", o Llei d'Ohm per als curiosos

Fins i tot l’últim pastís, després d’haver estudiat durant un cert temps a la desena nota, li dirà al professor que Ohm's law - això és “U és igual a I vegades R”. Malauradament, l'estudiant excel·lent més intel·ligent dirà poc més, la part física de la llei d'Ohm continuarà sent un misteri per a set segells. Em permeto compartir amb els companys la meva experiència en presentar aquest tema aparentment primitiu.

L’objecte de la meva activitat pedagògica va ser l’art i la humanitat del 10è grau, els principals interessos que, com endevina el lector, es troben molt lluny de la física. És per això que l’ensenyament d’aquesta assignatura va ser confiat a l’autor d’aquestes línies, que, en general, ensenya biologia. Va ser fa uns anys.

La lliçó sobre la llei d'Ohm comença amb la afirmació trivial que el corrent elèctric és el moviment de les partícules carregades en un camp elèctric. Si només una força elèctrica actua sobre una partícula carregada, la partícula s'accelerarà segons la segona llei de Newton. I si el vector de força elèctrica que actua sobre la partícula carregada és constant en tota la trajectòria, és igualment accelerat. Igual que un pes cau sota la influència de la gravetat.

Però aquí el paracaigudista cau completament malament. Si descuidem el vent, la seva velocitat de caiguda és constant. Fins i tot un estudiant de la classe d'art i humanitari respondrà que, a més de la força de la gravetat, una força més actua sobre el paracaigudes que cau: la força de la resistència aèria. Aquesta força és igual a un valor absolut que la força d'atracció del paracaigudes per la Terra i és oposada a la seva direcció. Per què? Aquesta és la pregunta clau de la lliçó. Després d'alguna discussió, arribem a la conclusió que la força d'arrossegament augmenta amb un ritme de caiguda creixent. Per tant, el cos que cau s’accelera fins a una velocitat a la qual s’equipara la gravetat i la resistència a l’aire, i el cos encara cau a una velocitat constant.

És cert que, en el cas d’un paracaigudista, la situació és una mica més complicada. El paracaigudes no s’obre immediatament i el paracaigudista s’accelera fins a una velocitat significativament superior. I quan el paracaigudes ja s'ha obert, la caiguda comença amb un alentiment, que es continua fins a equilibrar la força de gravetat i la força de resistència de l'aire.

Per a una càrrega de paracaigudes amb una massa total m descendint a una velocitat constant v, podem escriure: mg - F (v) = 0, on F (v) És la força de resistència de l'aire, considerada com una funció de la velocitat de caiguda. Respecte a la forma de la funció F (v) només podem dir una cosa fins ara: està creixent de manera monòtona. És aquesta circumstància la que proporciona estabilització de la velocitat.

En el cas més senzill, quan F (v) = k, la velocitat constant amb la qual caurà el paracaigudes serà igual a mg / k. Anem a fer una mica de conversió ara. Que el paracaigudes caigui des de l’altura h. Aleshores, la diferència en les energies potencials del cos abans i després de la caiguda serà igual a mgh = mU, on U és l’energia potencial d’un cos de massa d’unitat a una alçada h, o la diferència de potencial del camp gravitatori als punts inicials i finals d’incidència.

A la vista de l'anterior, obtenim la fórmula: F (v) = mU / h. (1)

I tornem ara al conductor pel qual flueix el corrent elèctric. Un gran nombre de partícules carregades es mouen al llarg del conductor, que xoquen amb els àtoms més sovint, més ràpidament volen. L’analogia amb la baixada d’un paracaigudes és força transparent, l’única diferència és que hi ha molts “paracaigudes” i no es mouen en el camp gravitatori, sinó en el camp elèctric. Tenint en compte aquestes circumstàncies, (1) es pot reescriure en la forma: F (v) = eU / l, (2)

on e és la càrrega de partícules, U és la diferència de potencial elèctric als extrems del conductor, l és la longitud del conductor.La força actual és òbviament igual a I = neS, on n és el nombre de partícules carregades per unitat de volum, S és l’àrea de secció del conductor, és la velocitat de la partícula (per senzillesa, suposem que totes les partícules carregades són iguals).

Per obtenir la dependència I (U), cal conèixer explícitament la dependència F (). L’opció més simple (F = k) dóna immediatament la llei d’Ohm (I ~ U):

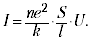
El valor s'anomena conductivitat i la reciprocitat d'aquest es diu resistència. En honor al descobridor de la llei, la resistència s’expressa normalment en ohms.

El valor (ne2 / k) s’anomena conductivitat específica i el seu valor invers s’anomena resistència específica. Aquests valors caracteritzen el material en què consisteix el conductor. És significatiu que la conductivitat sigui proporcional al nombre de partícules carregades per unitat de volum (n). En solucions de metalls i electròlits, aquest nombre és gran, però en dielectrics és petit. El nombre de partícules carregades per volum de unitat de gas pot dependre del camp aplicat (és a dir, és funció de U), per tant, la llei Ohm no s'aplica als gasos.

Al derivar la llei d’Ohm, vam fer una suposició no evident. Vam acceptar que la força que inhibeix el moviment d’una partícula carregada és proporcional a la seva velocitat. Per descomptat, es podria intentar justificar d’alguna manera aquesta idea, però la verificació experimental sembla molt més convincent.

Una verificació experimental d’aquest supòsit és, òbviament, una verificació de la pròpia llei d’Ohm, és a dir. proporcionalitat d'U i jo. Sembla que això no és difícil de fer: tenim un voltímetre i un amperímetre. Per desgràcia, tot no és tan senzill. Hem d’explicar als nostres estudiants que un voltímetre, igual que un amperímetre, no mesura la tensió, sinó la força actual. I tenim dret a establir volts només a l’escala de voltímetre només perquè inicialment coneixem la llei d’Ohm, que volem comprovar. Necessiteu altres enfocaments.

Podeu, per exemple, fer servir la idea següent. Connectem n bateries en sèrie i suposem que la tensió en aquest cas ha augmentat n vegades. Si la llei d'Ohm és certa, la força actual també augmentarà n vegades, a causa de la qual la relació n / I (n) no dependrà de n. Aquest supòsit es justifica per experiència. És cert que les bateries també tenen resistència interna, és per això que el valor de n / I (n) creix lentament a mesura que augmenta n, però no és difícil corregir-ho. (El mateix G. Ohm va mesurar l’estrès d’una manera diferent, que els estudiants poden llegir al llibre de text de G.Ya. Myakishev i altres.)

Ens fem la pregunta: "" A la llunyana constel·lació de Tau Ceti ", no la llei d'Ohm, sinó la llei del gran científic local Acadèmic X. Segons la llei de X, la força actual és proporcional al quadrat de la diferència de potencial als extrems del conductor. Com depèn la força de frenada de les partícules en funció de la seva velocitat del Tau Ceti? " Amb l’ajuda de transformacions simples, els estudiants arriben a la conclusió que la força és proporcional a l’arrel quadrada de la velocitat.

I ara passem a un altre procés: el moviment de l’aigua en una canonada, als extrems dels quals es creen diferents pressions. Aquí tenim una situació completament diferent: no les partícules mòbils individuals es freguen contra un material estacionari distribuït al llarg de tot el volum del conductor, sinó que les capes de partícules en moviment es freguen les unes contra les altres. I aquesta circumstància canvia fonamentalment tot el raonament físic.

Dues forces actuen sobre una capa separada d'aigua que es mou en una canonada:

a) la diferència de forces de pressió als extrems de la capa;

b) la força de fregament contra les capes d’aigua veïnes.

Si s'estableix una velocitat constant de la capa, aquestes forces són iguals i es dirigeixen en direccions oposades.

La força de fregament contra les capes d’aigua veïnes pot frenar el moviment si i només si diferents capes d’aigua es mouen a diferents velocitats. En un conductor, la velocitat de les partícules carregades no depèn de si estan a la vora del conductor o al seu centre, però l’aigua al centre de la canonada es mou ràpidament i lentament per les vores, a la mateixa superfície de la canonada, la velocitat de l’aigua és zero.

Un analògic de la força actual es pot considerar el flux d'aigua, és a dir. la quantitat d'aigua que surt de la canonada per unitat de temps. Com que la velocitat de l’aigua en diferents capes no és la mateixa, calcular el cabal no és tan senzill.Un analògic de la diferència de potencials elèctrics és la diferència de pressió als extrems del tub.

Igual que en un conductor amb corrent, s’observa una proporcionalitat directa a la canonada amb aigua entre la diferència de pressió als extrems i el cabal. Però el coeficient de proporcionalitat és completament diferent. Primer, el cabal d’aigua depèn no només de l’àrea de secció de la canonada, sinó també de la seva forma. Si la canonada és cilíndrica, el cabal és directament proporcional no a la secció de secció, sinó al seu quadrat (és a dir, al radi fins al quart grau). Aquesta dependència s’anomena llei Poiseuille.

Aquí és el moment de rememorar el curs d’anatomia, fisiologia i higiene, estudiat al novè grau. El cos humà té un gran nombre de vaixells connectats en paral·lel. Suposem que un d’aquests vaixells s’ha ampliat i el seu radi ha augmentat lleugerament, només s’ha duplicat. Quantes vegades, amb la mateixa pressió als extrems del vas, augmentarà la quantitat de sang que el travessa? L'àrea de secció transversal és proporcional al quadrat del radi, i el quadrat de la secció transversal és proporcional al radi de quart grau. Per tant, quan el radi es duplica, el flux sanguini augmenta 16 (!) Vegades. Aquesta és la potència de la llei Poiseuille, que ens permet crear un mecanisme molt eficaç per redistribuir la sang entre els òrgans. Si els electrons no passessin pels vasos sanguinis, però el seu flux augmentaria només quatre vegades.

La descripció del tema descrit anteriorment és diferent del tradicional. En primer lloc, es dediquen tres lliçons sobre el tema que, amb l'escassetat actual d'hores, es pot considerar un luxe inadmissible per a les ciències naturals. Tot i això, això es justifica pel fet que és possible revelar de manera senzilla i popular el significat físic de la llei i dotar als estudiants d’una metodologia que puguin utilitzar per analitzar una varietat de processos físics: la caiguda d’un cos a l’aire, el moviment d’un fluid en una canonada, el moviment de les partícules carregades al llarg d’un conductor i, posteriorment, en l'anàlisi del pas del corrent elèctric a través del buit i a través dels gasos.

Aquest enfocament s’anomena integració intradisciplinària. Amb la seva ajuda, vam demostrar als estudiants trets comuns a les seccions de la física distants, a primera vista, vam demostrar que la física no és un "grup" de "lleis físiques" que no estan connectades entre elles, sinó un edifici esvelt. El mateix passa, per descomptat, per a altres disciplines científiques. Així, sembla, una pèrdua irracional d’hores de formació està donant els seus fruits.

Llegiu també:Com utilitzar un multímetre